Definitionen in der Mathematik SoSe 18: Unterschied zwischen den Versionen
K (→Entwicklung einer "neuen" Definition) |
*m.g.* (Diskussion | Beiträge) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> | ||
| + | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| + | | valign="top" | | ||
| + | |||
==Was ist eine Definition?== | ==Was ist eine Definition?== | ||
*Eine Definition ist in der Mathematik eine Begriffsbestimmung, die nur aus Grundbegriffen oder bereits definierten Begriffen besteht.<br /> | *Eine Definition ist in der Mathematik eine Begriffsbestimmung, die nur aus Grundbegriffen oder bereits definierten Begriffen besteht.<br /> | ||
| Zeile 59: | Zeile 63: | ||
====Definition E.1: Ellipse==== | ====Definition E.1: Ellipse==== | ||
| + | |||
| + | Eine Ellipse ist die Menge aller Punkte, für die gilt |F1P| + |F2P|= Cons. und F1, F2 und P liegen in genau einer Ebene. | ||
| + | F1 und F2 heißen Brennpunkte der Ellipse. | ||
... | ... | ||
#Können Sie nun den Begriff Kreis unter Verwendung des Oberbegriffs Ellipse definieren?<br /> | #Können Sie nun den Begriff Kreis unter Verwendung des Oberbegriffs Ellipse definieren?<br /> | ||
| Zeile 64: | Zeile 71: | ||
====Definition K.1: Kreis als spezielle Ellipse==== | ====Definition K.1: Kreis als spezielle Ellipse==== | ||
| + | |||
| + | Ein Kreis ist eine Ellipse, für die gilt F1 = F2. | ||
... | ... | ||
| + | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
| + | |} | ||
| + | </div> | ||
| + | [[Kategorie:Einführung_S]] | ||
[[Category:Geo_P]] | [[Category:Geo_P]] | ||
Aktuelle Version vom 20. Oktober 2019, 11:42 Uhr
Was ist eine Definition?
Genau dasselbe, nur ganz anders: Arten, Definitionen zu formulierenEs gibt verschiedene Arten, Definitionen zu formulieren. Beispiel 1: ggT zweier ganzer ZahlenDie Begriffe Teiler und Euklidischer Algorithmus seien im Folgenden bereits exakt definiert. Das Übliche, die Realdefinition
Konventionaldefinition, das Ganze in "wenn-dann"
Schön, aber wie bekomme ich den ggT: die genetisch, operative Definition
Beispiel 2: DrachenviereckDie Begriffe Dreieck, Viereck, Diagonale, Eckpunkt, Geradenspiegelung und achsensymmetrisch seien im Folgenden bereits definiert. Realdefinition
Konventionaldefinition
genetisch, operative Definition
Ein wenig Didaktik: Definitionen auf verschiedenen NiveaustufenAus didaktischer Sicht lassen sich Definitionen auf verschiedenen Niveaustufen formulieren.
Entwicklung einer "neuen" DefinitionIm Folgenden wollen wir versuchen, den (ihnen vermutlich wenig geläufigen) Begriff Ellipse zu definieren. Konstruktiv lässt sich eine Ellipse mit Hilfe der sogenannten Gärtnerkonstruktion, wie im folgenden Video, erzeugen.
Aufgaben:
Definition E.1: EllipseEine Ellipse ist die Menge aller Punkte, für die gilt |F1P| + |F2P|= Cons. und F1, F2 und P liegen in genau einer Ebene. F1 und F2 heißen Brennpunkte der Ellipse. ...
Vereinbarung: Wir setzen ebene Geometrie voraus. Definition K.1: Kreis als spezielle EllipseEin Kreis ist eine Ellipse, für die gilt F1 = F2. ... |
 und
und  zwei ganze Zahlen.
zwei ganze Zahlen. 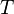 sei die Menge aller Zahlen, die sowohl Teiler von
sei die Menge aller Zahlen, die sowohl Teiler von  sowohl die ganze Zahl
sowohl die ganze Zahl  gibt, die auch
gibt, die auch  ein Dreieck und
ein Dreieck und 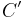 das Bild von
das Bild von  bei der Spiegelung an
bei der Spiegelung an  . Das Viereck
. Das Viereck 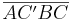 ist ein Drachenviereck.
ist ein Drachenviereck.

