Übungsaufgaben zur Algebra, Serie 2 SoSe 2018: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 2.5) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 2.7) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 25: | Zeile 25: | ||
=Aufgabe 2.6= | =Aufgabe 2.6= | ||
Es sei <math>[ G, \circ]</math> eine Gruppe. Beweisen Sie: Wenn <math>e \in G</math> das Linkseinselement von <math>[ G, \circ]</math> ist, dann ist <math>e</math> auch das Rechtseinselement von <math>[ G, \circ]</math>. | Es sei <math>[ G, \circ]</math> eine Gruppe. Beweisen Sie: Wenn <math>e \in G</math> das Linkseinselement von <math>[ G, \circ]</math> ist, dann ist <math>e</math> auch das Rechtseinselement von <math>[ G, \circ]</math>. | ||
| + | =Aufgabe 2.7= | ||
| + | Beweisen Sie die Eindeutigkeit des Einselementes für Gruppen. | ||
| + | =Aufgabe 2.8= | ||
| + | Beweisen Sie: In jeder Gruppe hat jedes Gruppenelement genau ein inverses Element.[\mat | ||
| + | =Aufgabe 2.9= | ||
| + | Beweisen Sie: In jeder Gruppe <math>[G, \circ]</math> sind die Gleichungen <br /> | ||
| + | <math>\begin{align} a \circ x &= b \\ y \circ a &= b \end{align}</math><br /> | ||
| + | eindeutig Lösbar. | ||
| + | =Aufgabe 2.10= | ||
| + | In jeder Gruppe sind die in Aufgabe 2.9 genannten Gleichungen immer eindeutig lösbar. In den Modulen der natürlichen Zahlen mit der Multiplikation bzw. mit der Addition sind die genannten Gleichungen nicht immer lösbar. Eine Gemeinsamkeit bzgl. der Lösbarkeit der Gleichungen haben diese Module allerdings mit Gruppen gemeinsam. Welche? Diese Eigenschaft heißt im übrigen Regularität. <math>[\mathbb{N}, + ]</math> und <math>[\mathbb{N}, \cdot ]</math> sind kommutative, reguläre Halbgruppen mit Einslement. | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Algebra]] | [[Kategorie:Algebra]] | ||
Aktuelle Version vom 1. Mai 2018, 15:29 Uhr
Aufgabe 2.1Gegeben sei Bestimmen Sie Aufgabe 2.2Bestimmen Sie die Verknüpfungstafel der Gruppe Aufgabe 2.3Es sei Aufgabe 2.4Beweisen Sie: Bis auf Strukturgleicheit gibt es zwei und nur zwei verschiedene vierelementige Gruppen. Aufgabe 2.5Es sei Aufgabe 2.6Es sei Aufgabe 2.7Beweisen Sie die Eindeutigkeit des Einselementes für Gruppen. Aufgabe 2.8Beweisen Sie: In jeder Gruppe hat jedes Gruppenelement genau ein inverses Element.[\mat Aufgabe 2.9Beweisen Sie: In jeder Gruppe Aufgabe 2.10In jeder Gruppe sind die in Aufgabe 2.9 genannten Gleichungen immer eindeutig lösbar. In den Modulen der natürlichen Zahlen mit der Multiplikation bzw. mit der Addition sind die genannten Gleichungen nicht immer lösbar. Eine Gemeinsamkeit bzgl. der Lösbarkeit der Gleichungen haben diese Module allerdings mit Gruppen gemeinsam. Welche? Diese Eigenschaft heißt im übrigen Regularität. |
![DD_\Delta:=\left [ \left \{ \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix}, \begin{pmatrix} -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} \sqrt{3} & -\frac{1}{2} \sqrt{3} \\ \end{pmatrix}, \begin{pmatrix} a & b \\ c & d \end{pmatrix} \right \}, \circ \right ]](/images/math/5/f/2/5f20e500bcab3995ec3dca6e5a97b976.png) .
. 
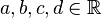 derart, dass
derart, dass 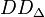 eine Gruppe ist. Die Operation
eine Gruppe ist. Die Operation  ist dabei als die normale Matrizenmultiplikation zu verstehen.
ist dabei als die normale Matrizenmultiplikation zu verstehen.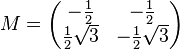
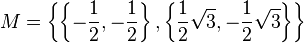 .
. 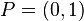 ein. Lassen Sie nun
ein. Lassen Sie nun 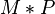 berechnen. Es wird eine Bildpunkt von
berechnen. Es wird eine Bildpunkt von  berechnet ... .
berechnet ... .
![\left [ \mathbb{Z}_3, \oplus \right ].](/images/math/e/4/a/e4a389d44643737f1da42498de82504a.png) (Restklassen modulo 3, mit Restklassenadddition). Vergleichen Sie mit der Gruppentafel aus Aufgabe 2.1.
(Restklassen modulo 3, mit Restklassenadddition). Vergleichen Sie mit der Gruppentafel aus Aufgabe 2.1.
![\left [ \left \{ e, a, b \right \}, \circ \right ]](/images/math/8/f/e/8fefe6155e950bd69ee5f8780c6a3679.png) eine Gruppe mit dem Einselement
eine Gruppe mit dem Einselement  .
. muss das Inverse von
muss das Inverse von  und
und ![[ G, \circ]](/images/math/4/6/8/4686bbf90bf7ebab892b288a31255920.png) eine Gruppe. Beweisen Sie: Wenn
eine Gruppe. Beweisen Sie: Wenn 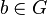 das Rechtsinverse zu
das Rechtsinverse zu 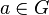 ist, dann ist
ist, dann ist 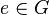 das Linkseinselement von
das Linkseinselement von 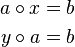
![[\mathbb{N}, + ]](/images/math/c/b/0/cb0c8e104771b0f88f88c4c0feb081c8.png) und
und ![[\mathbb{N}, \cdot ]](/images/math/8/f/d/8fd4f4229f12df9ff0dc9d1e91688c5f.png) sind kommutative, reguläre Halbgruppen mit Einslement.
sind kommutative, reguläre Halbgruppen mit Einslement.

