Begriff der Relation: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Der Vater ist immer der Gärtner, ein Video) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
| − | == | + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#CCFFCC; align:left;"> |
| + | {|width=90%| style="background-color:#CCFFCC; padding:1em" | ||
| + | | valign="top" | | ||
| + | <!--- Was hier drüber steht muss stehen bleiben ---> | ||
| + | = Relationen = | ||
| − | + | == Beispiele == | |
| − | + | === Halt dich senkrecht=== | |
[[File:Flag of Switzerland (Pantone).svg|thumb|Flag of Switzerland (Pantone)]]<br /> | [[File:Flag of Switzerland (Pantone).svg|thumb|Flag of Switzerland (Pantone)]]<br /> | ||
Im Schulpraktikum war der Begriff der Senkrechten zu behandeln. Der Praktikant hatte ein Bild der Schweizer Nationalflagge auf eine Folie gedruckt und fragte die Schüler, welche Linien Senkrechte wären. Bei den Schülern stellte sich nach den ersten Antworten leichte Unsicherheit ein. <br />Der Grund für diese Unsicherheit: Die Frage des Praktikanten war völlig unsinnig. Eine Antwort wie ''Gerade <math>a</math> steht senkrecht'' ist lediglich eine Aussageform, der kein Wahrheitswert zuzuordnen ist. Erst wenn man die Lage von <math>a</math> bezüglich einer anderen Geraden <math>b</math> (Ebene, Strahl, Strecke) betrachtet, ist es sinnvoll davon zu sprechen, dass <math>a</math> eine Senkrechte ist.<br />'''Die Relation Gerade <math>a</math> steht senkrecht auf Gerade <math>b</math> ist zweistellig.''' | Im Schulpraktikum war der Begriff der Senkrechten zu behandeln. Der Praktikant hatte ein Bild der Schweizer Nationalflagge auf eine Folie gedruckt und fragte die Schüler, welche Linien Senkrechte wären. Bei den Schülern stellte sich nach den ersten Antworten leichte Unsicherheit ein. <br />Der Grund für diese Unsicherheit: Die Frage des Praktikanten war völlig unsinnig. Eine Antwort wie ''Gerade <math>a</math> steht senkrecht'' ist lediglich eine Aussageform, der kein Wahrheitswert zuzuordnen ist. Erst wenn man die Lage von <math>a</math> bezüglich einer anderen Geraden <math>b</math> (Ebene, Strahl, Strecke) betrachtet, ist es sinnvoll davon zu sprechen, dass <math>a</math> eine Senkrechte ist.<br />'''Die Relation Gerade <math>a</math> steht senkrecht auf Gerade <math>b</math> ist zweistellig.''' | ||
| − | + | ===Eine klassische Dreiecksbeziehung=== | |
Tom ist der Liebhaber von Gabi. Zu der Ehre der Liebhabereigenschaft kommt er durch die Existenz von Frank, dem Ehemann von Gabi. Tom, Gabi und Frank stehen in einer dreistelligen Relation zueinander, der klassischen Dreiecksbeziehung.<br />Wir könnten diese Relation auch so formulieren: Gabi steht zwischen zwei Männern. | Tom ist der Liebhaber von Gabi. Zu der Ehre der Liebhabereigenschaft kommt er durch die Existenz von Frank, dem Ehemann von Gabi. Tom, Gabi und Frank stehen in einer dreistelligen Relation zueinander, der klassischen Dreiecksbeziehung.<br />Wir könnten diese Relation auch so formulieren: Gabi steht zwischen zwei Männern. | ||
| − | + | === Beispiel 3 === | |
Trauen Sie sich: Präsentieren Sie hier ein eigenes Beispiel. | Trauen Sie sich: Präsentieren Sie hier ein eigenes Beispiel. | ||
| − | + | === Ein Quiz zwischendurch === | |
<quiz> | <quiz> | ||
{Setzen Sie ein Häckchen, wenn es sich um eine <u>zweistellige</u> Relation handelt} | {Setzen Sie ein Häckchen, wenn es sich um eine <u>zweistellige</u> Relation handelt} | ||
| Zeile 26: | Zeile 30: | ||
</quiz> | </quiz> | ||
| − | + | = Definition des Begriffs der Relation = | |
<u>Definition: (<math>2</math>stellige Relation)</u> | <u>Definition: (<math>2</math>stellige Relation)</u> | ||
:::Es seien <math> M_1</math> und <math>M_2</math>Mengen, wobei keine dieser Mengen die leere Menge ist. Jede Teilmenge aus <math> M_1 \times M_2</math> ist eine <math>\ 2</math>stellige Relation. | :::Es seien <math> M_1</math> und <math>M_2</math>Mengen, wobei keine dieser Mengen die leere Menge ist. Jede Teilmenge aus <math> M_1 \times M_2</math> ist eine <math>\ 2</math>stellige Relation. | ||
<u>Definition: (n-stellige Relation)</u> | <u>Definition: (n-stellige Relation)</u> | ||
:::Es seien <math> M_1,\ M_2,\ M_3,\ ...,\ M_n\ n</math> Mengen, wobei keine dieser Mengen die leere Menge ist. Jede Teilmenge aus <math> M_1 \times M_2 \times M_3 ...\times M_n </math> ist eine <math>\ n-</math>stellige Relation. | :::Es seien <math> M_1,\ M_2,\ M_3,\ ...,\ M_n\ n</math> Mengen, wobei keine dieser Mengen die leere Menge ist. Jede Teilmenge aus <math> M_1 \times M_2 \times M_3 ...\times M_n </math> ist eine <math>\ n-</math>stellige Relation. | ||
| − | + | = Der Vater ist immer der Gärtner, ein Video zur Idee der Relation= | |
Meine ersten Versuche mit dem Medium, leider viel zu lang. <br /> | Meine ersten Versuche mit dem Medium, leider viel zu lang. <br /> | ||
--[[Benutzer:*m.g.*|*m.g.*]] ([[Benutzer Diskussion:*m.g.*|Diskussion]]) 14:51, 5. Mai 2018 (CEST)<br /> | --[[Benutzer:*m.g.*|*m.g.*]] ([[Benutzer Diskussion:*m.g.*|Diskussion]]) 14:51, 5. Mai 2018 (CEST)<br /> | ||
<iframe width="560" height="315" src="https://www.youtube.com/embed/wv_Z9jRxWVM" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> | <iframe width="560" height="315" src="https://www.youtube.com/embed/wv_Z9jRxWVM" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> | ||
| + | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
| + | |} | ||
| + | </div> | ||
| + | [[Kategorie:Algebra]] | ||
Aktuelle Version vom 5. Mai 2018, 13:55 Uhr
RelationenBeispieleHalt dich senkrechtDatei:Flag of Switzerland (Pantone).svg Flag of Switzerland (Pantone) Im Schulpraktikum war der Begriff der Senkrechten zu behandeln. Der Praktikant hatte ein Bild der Schweizer Nationalflagge auf eine Folie gedruckt und fragte die Schüler, welche Linien Senkrechte wären. Bei den Schülern stellte sich nach den ersten Antworten leichte Unsicherheit ein. Eine klassische DreiecksbeziehungTom ist der Liebhaber von Gabi. Zu der Ehre der Liebhabereigenschaft kommt er durch die Existenz von Frank, dem Ehemann von Gabi. Tom, Gabi und Frank stehen in einer dreistelligen Relation zueinander, der klassischen Dreiecksbeziehung. Beispiel 3Trauen Sie sich: Präsentieren Sie hier ein eigenes Beispiel.
Ein Quiz zwischendurch
Definition des Begriffs der RelationDefinition: (
Definition: (n-stellige Relation)
Der Vater ist immer der Gärtner, ein Video zur Idee der RelationMeine ersten Versuche mit dem Medium, leider viel zu lang. [ www.youtube.com is not an authorized iframe site ] |
 steht senkrecht ist lediglich eine Aussageform, der kein Wahrheitswert zuzuordnen ist. Erst wenn man die Lage von
steht senkrecht ist lediglich eine Aussageform, der kein Wahrheitswert zuzuordnen ist. Erst wenn man die Lage von  (Ebene, Strahl, Strecke) betrachtet, ist es sinnvoll davon zu sprechen, dass
(Ebene, Strahl, Strecke) betrachtet, ist es sinnvoll davon zu sprechen, dass 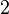 stellige Relation)
stellige Relation)
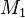 und
und  Mengen, wobei keine dieser Mengen die leere Menge ist. Jede Teilmenge aus
Mengen, wobei keine dieser Mengen die leere Menge ist. Jede Teilmenge aus 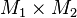 ist eine
ist eine 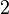 stellige Relation.
stellige Relation.
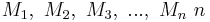 Mengen, wobei keine dieser Mengen die leere Menge ist. Jede Teilmenge aus
Mengen, wobei keine dieser Mengen die leere Menge ist. Jede Teilmenge aus 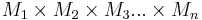 ist eine
ist eine 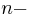 stellige Relation.
stellige Relation.

