Allgemeine lineare Gleichung mit drei Variablen: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#B9D0F0; align:left;"> {|width=90%| style="backgro…“) |
*m.g.* (Diskussion | Beiträge) (→Beispiel 1) |
||
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
| valign="top" | | | valign="top" | | ||
<!--- hier drüber nichts eintragen ---> | <!--- hier drüber nichts eintragen ---> | ||
| − | + | ===Allgemeine lineare Gleichung ax + by + cz = d=== | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | ===ax + by + cz = d=== | + | |
<math> | <math> | ||
\begin{align} | \begin{align} | ||
| Zeile 17: | Zeile 13: | ||
===Grafische Veranschaulichung der Lösungsmenge einer Gleichung vom Typ ax+by+cz=d=== | ===Grafische Veranschaulichung der Lösungsmenge einer Gleichung vom Typ ax+by+cz=d=== | ||
| − | Es seien <math>a, b, c \in \mathbb{R}</math> , beliebig aber fest, <math>a, b</math> nicht gleichzeitig <math>0</math>,<br /> | + | ====Gerade?==== |
| − | <math>x,y \in \mathbb{R}</math>, variabel.<br /> Wir untersuchen die Gleichung<br /> | + | Es seien <math>a, b, c, d \in \mathbb{R}</math> , beliebig aber fest, <math>a, b, c</math> nicht gleichzeitig <math>0</math>,<br /> |
| − | + | <math>x,y,z \in \mathbb{R}</math>, variabel.<br /> Wir untersuchen die Gleichung<br /> | |
| + | <math>ax+by+cz=d</math><br /> | ||
| + | Die Lösungsmenge einer Gleichung vom Typ <math>ax+by=c</math> ließ sich die Koordinaten der Punkte einer Geraden im <math>\mathbb{R}^2</math> interpretieren. | ||
| + | Man mag schnell geneigt sein, die Lösungsmenge der Gleichung <math>ax+by+cz=d</math> alsdie Koordinaten einer Geraden im Raum <math>\mathbb{R}^3</math> zu interpretieren. Dem ist aber nicht so:<br /> | ||
| + | ====Spezialfall: zwei der Koeffizieneten, a, b, c sind gleich 0==== | ||
| + | Sei etwa nur der Koeffizient <math>a</math> verschieden von <math>0</math>. In diesem Fall vereinfacht sich unsere Gleichung zu <math>ax=d</math>. Umgestellt nach <math>x</math> ergibt sich <math>x=\frac{d}{a}</math>. Alle geordneten Tripel <math>\left (\frac{d}{a}, y, z \right )</math> aus dem <math>\mathbb{R}^3</math> genügen damit unserer Gleichung.<br /> | ||
| + | Unklar? Wir können die Gleichung auch als <math>ax+0y+0z=d</math> bzw. <math>x + 0y + 0z = \frac{d}{a}</math> schreiben.<br /> | ||
| + | Die Lösungsmenge dieser Gleichung lässt sich als die Koordinatentripel der Punkte einer Ebene <math>\varepsilon</math> interpretieren, die parallel zu einer der Koordinatenebene ist: | ||
| + | * Die Lösungsmenge der Gleichung <math>2x + 0y+ 0z = 3</math> sind die Koordinatentripel aller Punkte der Ebene, die parallel zur <math>y-z-</math>Ebene ist und durch den Punkt mit den Koordinaten <math>\left ( \frac{3}{2} \right )</math> geht. | ||
| + | * Die Lösungsmenge der Gleichung <math>0x +\frac{3}{7}y + 0z= \frac{5}{3}</math> sind die Koordinatentripel aller Punkte der Ebene, die parallel zur <math>x-z-</math>Ebene ist und durch den Punkt mit den Koordinaten <math>\left ( 0, \frac{35}{9} \right )</math> geht. | ||
| + | * Die Lösungsmenge der Gleichung <math>0x + 0y + \pi z = 0</math> ist die <math>x-y-</math>Ebene. | ||
| + | ====Spezialfall: einer der drei Koeffizienten a, b, c ist gleich 0==== | ||
| + | =====Beispiel 1===== | ||
| + | <math>z=0</math>, <math>a=2</math>, <math>c=\frac{3}{5}</math>, <math>d=1</math><br /> | ||
| − | '''Satz | + | Unsere Gleichung lautet für dieses Beispiel <math>2x+\frac{3}{5}y+0z=1</math><br /> |
| + | Die Bestimmung der Lösungsmenge dieser Gleichung vereinfacht sich zunächst zu einem ebenen Problem:<br /> | ||
| + | <math>2x+\frac{3}{5}y=1</math> Die Lösungsmenge dieser vereinfachten Gleichung ist eine Gerade in der <math>x-y-</math>Ebene. Im konkreten Fall handelt es sich um die Gerade mit der Gleichung <math>2x+\frac{3}{5}y=1</math> bzw. mit der Gleichung <math>y=-\frac{10}{3}x+\frac{5}{3}</math>. <br /> | ||
| + | Die Lösungsmenge unserer Ausgangsgleichung <math>2x+\frac{3}{5}y+0z=1</math> ist damit eine Ebene, die senkrecht auf der | ||
| + | <math>x-y-</math>Ebene steht und mit der <math>x-y-</math>Ebene die Gerade <math>y=-\frac{10}{3}x+\frac{5}{3}</math> gemeinsam hat. | ||
| + | |||
| + | ====Allgemeiner Fall: jeder der Koeffizienten a, b, c ist verschieden von 0 ==== | ||
| + | |||
| + | ====Ebene!==== | ||
| + | '''Satz:'''<br /> | ||
:Die Gleichung (II) <math>ax+by+cz=d</math> beschreibt die Menge aller Punkte einer Ebene im <math>\mathbb{R}^3</math>.<br /> | :Die Gleichung (II) <math>ax+by+cz=d</math> beschreibt die Menge aller Punkte einer Ebene im <math>\mathbb{R}^3</math>.<br /> | ||
| − | |||
Aktuelle Version vom 9. Mai 2018, 13:00 Uhr
Allgemeine lineare Gleichung ax + by + cz = d
Grafische Veranschaulichung der Lösungsmenge einer Gleichung vom Typ ax+by+cz=dGerade?Es seien Spezialfall: zwei der Koeffizieneten, a, b, c sind gleich 0Sei etwa nur der Koeffizient
Spezialfall: einer der drei Koeffizienten a, b, c ist gleich 0Beispiel 1
Unsere Gleichung lautet für dieses Beispiel Allgemeiner Fall: jeder der Koeffizienten a, b, c ist verschieden von 0Ebene!Satz:
|
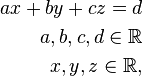
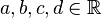 , beliebig aber fest,
, beliebig aber fest, 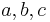 nicht gleichzeitig
nicht gleichzeitig 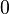 ,
,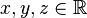 , variabel.
, variabel.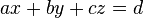
 ließ sich die Koordinaten der Punkte einer Geraden im
ließ sich die Koordinaten der Punkte einer Geraden im 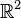 interpretieren.
Man mag schnell geneigt sein, die Lösungsmenge der Gleichung
interpretieren.
Man mag schnell geneigt sein, die Lösungsmenge der Gleichung 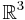 zu interpretieren. Dem ist aber nicht so:
zu interpretieren. Dem ist aber nicht so: verschieden von
verschieden von 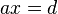 . Umgestellt nach
. Umgestellt nach 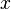 ergibt sich
ergibt sich 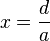 . Alle geordneten Tripel
. Alle geordneten Tripel 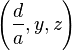 aus dem
aus dem 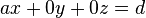 bzw.
bzw. 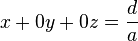 schreiben.
schreiben. interpretieren, die parallel zu einer der Koordinatenebene ist:
interpretieren, die parallel zu einer der Koordinatenebene ist:
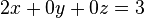 sind die Koordinatentripel aller Punkte der Ebene, die parallel zur
sind die Koordinatentripel aller Punkte der Ebene, die parallel zur 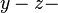 Ebene ist und durch den Punkt mit den Koordinaten
Ebene ist und durch den Punkt mit den Koordinaten  geht.
geht.
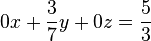 sind die Koordinatentripel aller Punkte der Ebene, die parallel zur
sind die Koordinatentripel aller Punkte der Ebene, die parallel zur 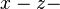 Ebene ist und durch den Punkt mit den Koordinaten
Ebene ist und durch den Punkt mit den Koordinaten 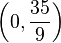 geht.
geht.
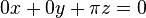 ist die
ist die 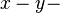 Ebene.
Ebene.
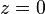 ,
, 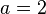 ,
, 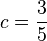 ,
, 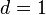
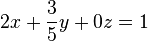
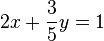 Die Lösungsmenge dieser vereinfachten Gleichung ist eine Gerade in der
Die Lösungsmenge dieser vereinfachten Gleichung ist eine Gerade in der 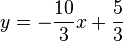 .
. 
