Übungsaufgaben zur Algebra, Serie 4 SoSe 2018: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 4.2) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 4.10) |
||
| (13 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
=Aufgabe 4.2= | =Aufgabe 4.2= | ||
| − | Die Gleichung <math>a_2x+b_2y=c_2</math> ist eine Linearkombination der Gleichung <math>a_1x+b_1y=c_1</math>, wenn eine Zahl <math>\lambda \in \mathbb{R}</math> derart | + | Die Gleichung <math>a_2x+b_2y=c_2</math> ist eine ''Linearkombination'' der Gleichung <math>a_1x+b_1y=c_1</math>, wenn eine Zahl <math>\lambda \in \mathbb{R}</math> derart existiert, |
dass <br /> | dass <br /> | ||
<math>\begin{matrix} \lambda a_1 &=& a_2 \\ \lambda b_1 &=& b_2 \\ \lambda c_1 &=& c_2 \end{matrix}</math> <br /> | <math>\begin{matrix} \lambda a_1 &=& a_2 \\ \lambda b_1 &=& b_2 \\ \lambda c_1 &=& c_2 \end{matrix}</math> <br /> | ||
| − | gilt. | + | gilt.<br /> |
| + | (a) Beweisen Sie: Die Relation ''Gleichung b ist Linearkombination von Gleichung a'' ist eine Äquivalenzrelation auf der Menge der Gleichungen vom Typ <math>ax +by=c</math>.<br /> | ||
| + | (b) Interpretieren Sie die Relation geometrisch. | ||
=Aufgabe 4.3= | =Aufgabe 4.3= | ||
| − | + | Es sei <math>G_2</math> die Menge aller Gleichungen vom Typ <math>ax+by=c</math>. <math>\mathbb{G}</math> sei die Menge aller Äquivalenzklassen <math>\overline{g}</math>, in die <math>G</math> durch die Äquivalenzrelation ''Gleichung a ist Linearkombination von Gleichung b'' eingeteilt wird. Wir definieren auf <math>\mathbb{G}</math> die folgende Operation <math>\oplus</math>: <math>\forall \overline{a}, \overline{b} \in \mathbb{G}: \overline{a} \oplus \overline{b} := \overline{a+b}</math>. Beweisen Sie: <math>[\mathbb{G}, \oplus]</math> ist Gruppe. | |
=Aufgabe 4.4= | =Aufgabe 4.4= | ||
| − | + | Es sei <math>\mathbb{N}</math> die Menge der natürlichen Zahlen ohne die Zahl <math>0</math>. Wir definieren <math>\mathbb{B}:= \mathbb{N} \times \mathbb{N}</math>. Auf <math>\mathbb{B}</math> definieren wir die folgende Relation quotientengleich <math>=_q</math>: <math>\forall (a,b), (c,d) \in \mathbb{B}: (a,b)=_q(c,d) :\Leftrightarrow ad=bc</math>. Beweisen Sie <math>=_q</math> ist eine Äquivalenzrelation. | |
=Aufgabe 4.5= | =Aufgabe 4.5= | ||
| − | + | Es sei <math>\mathbb{Q}^+</math> die Menge aller Äquivalenzklassen <math>\overline{(a,b)}</math> in die <math>\mathbb{B}</math> durch <math>=_q</math> eingeteilt wird. Wir definieren <math>\overline{(a,b)} \odot \overline{(c,d)} := \overline{(ac,bd)}</math>. Beweisen Sie: <math>[\mathbb{Q}^+, \odot]</math> ist abelsche Gruppe. | |
=Aufgabe 4.6= | =Aufgabe 4.6= | ||
| − | + | Beweisen Sie: Die multiplikative Restklassengruppe modulo <math>7</math> ist zyklisch. Nennen Sie alle erzeugenden Elemente dieser Gruppe. | |
=Aufgabe 4.7= | =Aufgabe 4.7= | ||
| − | + | Nennen Sie eine multiplikative zyklische Gruppe, die genau vier erzeugende Elemente hat. | |
=Aufgabe 4.8= | =Aufgabe 4.8= | ||
| + | Wir betrachten <math>[\mathbb{R}, +]</math>, die additive Gruppe der reellen Zahlen. Unter <math>a^n, n\in \mathbb{Z}</math> verstehen wir somit das <math>n-</math>malige Aufaddieren von <math>a \in \mathbb{R}</math>. <math>a^{-1}</math> ist damit das inverse Element von <math>a</math> bzgl. der Addition reeller Zahlen.<br /> | ||
| + | Mittels dieser Potenzierung definieren wir für den <math>\mathbb{R}^2</math>: <math>\forall (a,b) \in \mathbb{R}^2, \forall n \in \mathbb{Z}: (a,b)^n:=(a^n,b^n)</math>.<br /> | ||
| + | Es sei <math>V_{12}:= \left \{(\sqrt{2},2)^n \vert n \in \mathbb{Z} \right \}</math>. Beweisen Sie, dass <math>\left [V_{12},\oplus \right ]</math> eine abelsche Gruppe ist. Unter <math>\oplus</math> verstehen wir dabei die übliche additive Verknüpfung von Elementen des <math>\mathbb{R}^2</math>. | ||
=Aufgabe 4.9= | =Aufgabe 4.9= | ||
| − | + | Beweisen Sie: Jede zyklische Gruppe ist abelsch. | |
=Aufgabe 4.10= | =Aufgabe 4.10= | ||
| − | + | Es sei <math>[\mathbb{Z}, +]</math> die Gruppe der ganzen Zahlen bezüglich der üblichen Addition auf <math>\mathbb{Z}</math>. <math>[2\mathbb{Z}, +]</math> sei die Gruppe der geraden Ganzen Zahlen bzgl. der üblichen Addition auf <math>\mathbb{Z}</math>. Wir definieren eine Abbildung <math>\varphi</math> von <math>\mathbb{Z}</math> auf <math>2\mathbb{Z}</math>: <math>\forall a \in \mathbb{Z}: \varphi (a):=a+a</math>. <br /> | |
| + | (a) Beweisen Sie: <math>\varphi</math> ist eine Bijektion<br /> | ||
| + | (b) <math>\forall a,b \in \mathbb{Z}: \varphi (a+b) = \varphi(a) + \varphi(b)</math>. | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
Aktuelle Version vom 13. Mai 2018, 11:40 Uhr
Aufgabe 4.1Wir betrachten auf der Menge der natürlichen Zahlen, die Relationen Teiler und echter Teiler. Aufgabe 4.2Die Gleichung Aufgabe 4.3Es sei Aufgabe 4.4Es sei Aufgabe 4.5Es sei Aufgabe 4.6Beweisen Sie: Die multiplikative Restklassengruppe modulo Aufgabe 4.7Nennen Sie eine multiplikative zyklische Gruppe, die genau vier erzeugende Elemente hat. Aufgabe 4.8Wir betrachten Es sei Aufgabe 4.9Beweisen Sie: Jede zyklische Gruppe ist abelsch. Aufgabe 4.10Es sei |
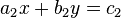 ist eine Linearkombination der Gleichung
ist eine Linearkombination der Gleichung 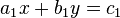 , wenn eine Zahl
, wenn eine Zahl 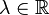 derart existiert,
dass
derart existiert,
dass 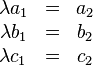
 .
.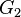 die Menge aller Gleichungen vom Typ
die Menge aller Gleichungen vom Typ 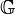 sei die Menge aller Äquivalenzklassen
sei die Menge aller Äquivalenzklassen 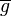 , in die
, in die  durch die Äquivalenzrelation Gleichung a ist Linearkombination von Gleichung b eingeteilt wird. Wir definieren auf
durch die Äquivalenzrelation Gleichung a ist Linearkombination von Gleichung b eingeteilt wird. Wir definieren auf  :
: 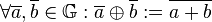 . Beweisen Sie:
. Beweisen Sie: ![[\mathbb{G}, \oplus]](/images/math/f/9/7/f973823fb9e00ff432d68505910909a8.png) ist Gruppe.
ist Gruppe.
 die Menge der natürlichen Zahlen ohne die Zahl
die Menge der natürlichen Zahlen ohne die Zahl 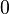 . Wir definieren
. Wir definieren 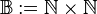 . Auf
. Auf 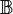 definieren wir die folgende Relation quotientengleich
definieren wir die folgende Relation quotientengleich 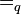 :
: 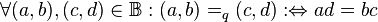 . Beweisen Sie
. Beweisen Sie 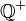 die Menge aller Äquivalenzklassen
die Menge aller Äquivalenzklassen 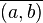 in die
in die 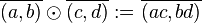 . Beweisen Sie:
. Beweisen Sie: ![[\mathbb{Q}^+, \odot]](/images/math/b/d/8/bd820b10ad4122ad5c5c8b8d1600aff7.png) ist abelsche Gruppe.
ist abelsche Gruppe.
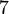 ist zyklisch. Nennen Sie alle erzeugenden Elemente dieser Gruppe.
ist zyklisch. Nennen Sie alle erzeugenden Elemente dieser Gruppe.
![[\mathbb{R}, +]](/images/math/b/c/d/bcda2db217cbfafb8f4e992cc54382c2.png) , die additive Gruppe der reellen Zahlen. Unter
, die additive Gruppe der reellen Zahlen. Unter 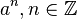 verstehen wir somit das
verstehen wir somit das 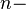 malige Aufaddieren von
malige Aufaddieren von 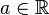 .
. 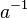 ist damit das inverse Element von
ist damit das inverse Element von  bzgl. der Addition reeller Zahlen.
bzgl. der Addition reeller Zahlen.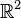 :
: 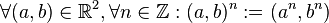 .
.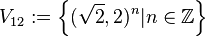 . Beweisen Sie, dass
. Beweisen Sie, dass ![\left [V_{12},\oplus \right ]](/images/math/8/4/5/845dd551d7abca7d64d41825e0a0de03.png) eine abelsche Gruppe ist. Unter
eine abelsche Gruppe ist. Unter ![[\mathbb{Z}, +]](/images/math/8/2/8/828d3197747f0dc881f51c684f1a4c7d.png) die Gruppe der ganzen Zahlen bezüglich der üblichen Addition auf
die Gruppe der ganzen Zahlen bezüglich der üblichen Addition auf 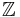 .
. ![[2\mathbb{Z}, +]](/images/math/2/e/e/2ee302fb5c070ca301bdf2fd7583d492.png) sei die Gruppe der geraden Ganzen Zahlen bzgl. der üblichen Addition auf
sei die Gruppe der geraden Ganzen Zahlen bzgl. der üblichen Addition auf  von
von 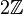 :
: 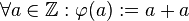 .
. 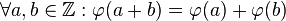 .
.

