Übungsaufgaben zur Algebra, Serie 4 SoSe 2018: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 4.7)
(→‎Aufgabe 4.10)
 
(3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 32: Zeile 32:
  
 
=Aufgabe 4.8=
 
=Aufgabe 4.8=
 +
Wir betrachten <math>[\mathbb{R}, +]</math>, die additive Gruppe der reellen Zahlen. Unter <math>a^n, n\in \mathbb{Z}</math> verstehen wir somit das <math>n-</math>malige Aufaddieren von <math>a \in \mathbb{R}</math>. <math>a^{-1}</math> ist damit das inverse Element von <math>a</math> bzgl. der Addition reeller Zahlen.<br />
 +
Mittels dieser Potenzierung definieren wir für den <math>\mathbb{R}^2</math>: <math>\forall (a,b) \in \mathbb{R}^2, \forall n \in \mathbb{Z}: (a,b)^n:=(a^n,b^n)</math>.<br />
  
 +
Es sei <math>V_{12}:= \left \{(\sqrt{2},2)^n \vert n \in \mathbb{Z} \right \}</math>. Beweisen Sie, dass <math>\left [V_{12},\oplus \right ]</math> eine abelsche Gruppe ist. Unter <math>\oplus</math> verstehen wir dabei die übliche additive Verknüpfung von Elementen des <math>\mathbb{R}^2</math>.
  
 
=Aufgabe 4.9=
 
=Aufgabe 4.9=
−
 
+
Beweisen Sie: Jede zyklische Gruppe ist abelsch.
  
 
=Aufgabe 4.10=
 
=Aufgabe 4.10=
−
 
+
Es sei <math>[\mathbb{Z}, +]</math> die Gruppe der ganzen Zahlen bezüglich der üblichen Addition auf <math>\mathbb{Z}</math>. <math>[2\mathbb{Z}, +]</math> sei die Gruppe der geraden Ganzen Zahlen bzgl. der üblichen Addition auf <math>\mathbb{Z}</math>. Wir definieren eine Abbildung <math>\varphi</math> von <math>\mathbb{Z}</math> auf <math>2\mathbb{Z}</math>: <math>\forall a \in  \mathbb{Z}: \varphi (a):=a+a</math>. <br />
 +
(a) Beweisen Sie: <math>\varphi</math> ist eine Bijektion<br />
 +
(b) <math>\forall a,b \in \mathbb{Z}: \varphi (a+b) = \varphi(a) + \varphi(b)</math>.
  
 
<!--- Was hier drunter steht muss stehen bleiben --->
 
<!--- Was hier drunter steht muss stehen bleiben --->

Aktuelle Version vom 13. Mai 2018, 11:40 Uhr

Inhaltsverzeichnis

Aufgabe 4.1

Wir betrachten auf der Menge der natürlichen Zahlen, die Relationen Teiler und echter Teiler.
(a) Eine dieser Relationen ist keine Äquivalenzrelationen. Welche? Beweisen Sie Ihre Aussage.
(b) Beweisen Sie für die andere Relation, dass sie eine Äquivalanzrelation ist.

Aufgabe 4.2

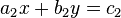Die Gleichung a_2x+b_2y=c_2 ist eine Linearkombination der Gleichung 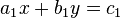a_1x+b_1y=c_1, wenn eine Zahl \lambda \in \mathbb{R} derart existiert, dass
\begin{matrix} \lambda a_1 &=& a_2 \\ \lambda b_1 &=& b_2 \\ \lambda c_1 &=& c_2 \end{matrix}
gilt.
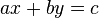(a) Beweisen Sie: Die Relation Gleichung b ist Linearkombination von Gleichung a ist eine Äquivalenzrelation auf der Menge der Gleichungen vom Typ ax +by=c.
(b) Interpretieren Sie die Relation geometrisch.

Aufgabe 4.3

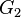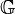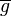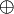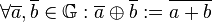Es sei G_2 die Menge aller Gleichungen vom Typ ax+by=c. \mathbb{G} sei die Menge aller Äquivalenzklassen \overline{g}, in die G durch die Äquivalenzrelation Gleichung a ist Linearkombination von Gleichung b eingeteilt wird. Wir definieren auf \mathbb{G} die folgende Operation \oplus: \forall \overline{a}, \overline{b} \in \mathbb{G}: \overline{a} \oplus \overline{b} := \overline{a+b}. Beweisen Sie: [\mathbb{G}, \oplus] ist Gruppe.

Aufgabe 4.4

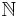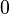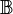Es sei \mathbb{N} die Menge der natürlichen Zahlen ohne die Zahl 0. Wir definieren \mathbb{B}:= \mathbb{N} \times \mathbb{N}. Auf \mathbb{B} definieren wir die folgende Relation quotientengleich 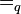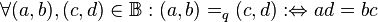=_q: \forall (a,b), (c,d) \in \mathbb{B}: (a,b)=_q(c,d) :\Leftrightarrow ad=bc. Beweisen Sie =_q ist eine Äquivalenzrelation.

Aufgabe 4.5

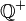Es sei \mathbb{Q}^+ die Menge aller Äquivalenzklassen 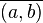\overline{(a,b)} in die 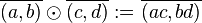\mathbb{B} durch =_q eingeteilt wird. Wir definieren \overline{(a,b)} \odot \overline{(c,d)} := \overline{(ac,bd)}. Beweisen Sie: [\mathbb{Q}^+, \odot] ist abelsche Gruppe.

Aufgabe 4.6

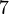Beweisen Sie: Die multiplikative Restklassengruppe modulo 7 ist zyklisch. Nennen Sie alle erzeugenden Elemente dieser Gruppe.

Aufgabe 4.7

Nennen Sie eine multiplikative zyklische Gruppe, die genau vier erzeugende Elemente hat.

Aufgabe 4.8

Wir betrachten [\mathbb{R}, +], die additive Gruppe der reellen Zahlen. Unter 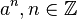a^n, n\in \mathbb{Z} verstehen wir somit das n-malige Aufaddieren von 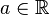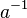a \in \mathbb{R}. a^{-1} ist damit das inverse Element von 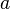a bzgl. der Addition reeller Zahlen.
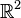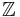Mittels dieser Potenzierung definieren wir für den \mathbb{R}^2: \forall (a,b) \in \mathbb{R}^2, \forall n \in \mathbb{Z}: (a,b)^n:=(a^n,b^n).

Es sei V_{12}:= \left \{(\sqrt{2},2)^n \vert n \in \mathbb{Z} \right \}. Beweisen Sie, dass \left [V_{12},\oplus \right ] eine abelsche Gruppe ist. Unter \oplus verstehen wir dabei die übliche additive Verknüpfung von Elementen des \mathbb{R}^2.

Aufgabe 4.9

Beweisen Sie: Jede zyklische Gruppe ist abelsch.

Aufgabe 4.10

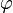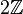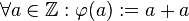Es sei [\mathbb{Z}, +] die Gruppe der ganzen Zahlen bezüglich der üblichen Addition auf \mathbb{Z}. [2\mathbb{Z}, +] sei die Gruppe der geraden Ganzen Zahlen bzgl. der üblichen Addition auf \mathbb{Z}. Wir definieren eine Abbildung \varphi von \mathbb{Z} auf 2\mathbb{Z}: \forall a \in \mathbb{Z}: \varphi (a):=a+a.
(a) Beweisen Sie: \varphi ist eine Bijektion
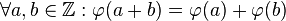(b) \forall a,b \in \mathbb{Z}: \varphi (a+b) = \varphi(a) + \varphi(b).

Von „http://geometrie.zum.de/index.php?title=Übungsaufgaben_zur_Algebra,_Serie_4_SoSe_2018&oldid=31497“