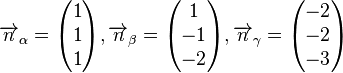Serie 4: größere LSG lösen SoSe 2018: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 4.6 SoSe 2018) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 4.10 SoSe 2018) |
||
| (5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 37: | Zeile 37: | ||
=Aufgabe 4.6 SoSe 2018= | =Aufgabe 4.6 SoSe 2018= | ||
Lösen Sie das folgende LGS, indem Sie es auf Diagonalenform bringen:<br /> | Lösen Sie das folgende LGS, indem Sie es auf Diagonalenform bringen:<br /> | ||
| − | <math>\begin{pmatrix} | + | <math>\begin{pmatrix} 15 & 3 & 7 & \vert & 10 \\ -4 & -10 & 4 & \vert & 4 \\ -2 & 1 & 2 & \vert & 11 \end{pmatrix} </math><br /> |
Da es um das Anwenden des Verfahrens geht, hier die Lösungsmenge:<br /> | Da es um das Anwenden des Verfahrens geht, hier die Lösungsmenge:<br /> | ||
| − | <math>\begin{pmatrix} 1 & ~ & ~ & \vert & - | + | <math>\begin{pmatrix} 1 & ~ & ~ & \vert & -\frac{111}{88} \\ ~ & 1 & ~ & \vert & \frac{3}{2} \\ ~ & ~& 1 & \vert & \frac{307}{88} \end{pmatrix} </math><br /> |
=Aufgabe 4.7 SoSe 2018= | =Aufgabe 4.7 SoSe 2018= | ||
| + | Gegeben seien die folgenden Punkte <math>A,B,C,D,E,F,H</math>:<br /> | ||
| + | <math> | ||
| + | \begin{matrix} | ||
| + | A &=& \begin{pmatrix} 1 \\ 1 \\ -1 \end{pmatrix} | ||
| + | B &=& \begin{pmatrix} -1 \\ 1 \\ -1 \end{pmatrix} | ||
| + | C &=& \begin{pmatrix} -1 \\ -1 \\ -1 \end{pmatrix} | ||
| + | D &=& \begin{pmatrix} 1 \\ -1 \\ -1 \end{pmatrix} \\ | ||
| + | E &=& \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} | ||
| + | F &=& \begin{pmatrix} -1 \\ 1 \\ 1 \end{pmatrix} | ||
| + | G &=& \begin{pmatrix} -1 \\ -1 \\ 1 \end{pmatrix} | ||
| + | H &=& \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} | ||
| + | \end{matrix} | ||
| + | </math><br /> | ||
| + | |||
| + | Wir betrachten einen Würfel mit den Eckpunkten <math>A,B,C,D,E,F,G,H</math>.<br /> | ||
| + | |||
| + | (a) Beschreiben Sie die Flächen dieses Würfels mittels Gleichungen vom Typ <math>ax+by+cz=d</math>.<br /> | ||
| + | (b) Beschreiben Sie die Geraden, die durch die Kanten des Würfels eindeutig bestimmt sind als Lösungsmenge jeweils eines Gleichungssystems. | ||
=Aufgabe 4.8 SoSe 2018= | =Aufgabe 4.8 SoSe 2018= | ||
| + | Wir drehen den Würfel aus Aufgabe 4.7 um die <math>z-</math>Achse mit einem Drehwinkel von <math>45^\circ</math> mathematisch positiv. Dabei werden die Eckpunkte unseres Würfels auf ihre Bilder <math>A',B',C',D',E',F',G',H'</math> abgebildet.<br /> | ||
| + | Geben Sie ein LGS an, das die Koordinaten des Punktes <math>D'</math> und nur die Koordinaten des Punktes <math>D'</math> als Lösungsmenge hat. | ||
=Aufgabe 4.9 SoSe 2018= | =Aufgabe 4.9 SoSe 2018= | ||
| + | Wir drehen den gedrehten Würfel aus Aufgabe 4.8 um die <math>y-</math>Achse mit einem Drehwinkel von <math>45^\circ</math> in mathematisch postivem Drehsinn.<br /> | ||
| + | Die Punkte <math>A',B',C',D',E',F',G',H'</math> werden jetzt auf die Punkte <math>A'',B'',C'',D'',E'',F'',G'',H''</math> abgebildet. | ||
| + | Bestimmen Sie eine Gleichung der Form <math>ax+by+cz=d</math> zur Beschreibung des Bildes der Grundfläche <math>\overline{A'',B'',C'',D''}</math> unseres Würfels. | ||
=Aufgabe 4.10 SoSe 2018= | =Aufgabe 4.10 SoSe 2018= | ||
| − | + | Oberstudienrat Kramer gibt seiner 13a die drei Ebenen <math>\alpha, \beta, \gamma</math> vor, wobei gelte <math>\alpha \cap \beta \cap \gamma = \left \{ \begin{pmatrix} 1 \\ 1 \\ -1 \end{pmatrix} \right \}</math>.<br /> | |
| + | Ferner gibt Oberstudienrat Kramer die folgenden Normalenvektoren der Ebenen vor:<br /> | ||
| + | <math>\overrightarrow{n}_\alpha=\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}, \overrightarrow{n}_\beta=\begin{pmatrix} 1 \\ -1 \\ -2 \end{pmatrix}, \overrightarrow{n}_\gamma=\begin{pmatrix} -2 \\ -2 \\ -3 \end{pmatrix}</math> <br /> | ||
| + | Lisa meint, dass das Blödsinn wäre. Hat sie recht oder will sie Oberstudienrat Kramer nur provozieren? | ||
<!--- hier drunter nichts eintragen ---> | <!--- hier drunter nichts eintragen ---> | ||
[[Kategorie:Linalg]] | [[Kategorie:Linalg]] | ||
Aktuelle Version vom 13. Mai 2018, 13:52 Uhr
Aufgabe 4.1 SoSe 2018Es seien
Aufgabe 4.2 SoSe 2018Geben Sie ein lineares Gleichungssystem vom Typ Aufgabe 4.3 SoSe 2018Beschreiben Sie die Gerade Aufgabe 4.5 SoSe 2018Lösen Sie das folgende LGS, indem Sie es auf Diagonalenform bringen: Aufgabe 4.6 SoSe 2018Lösen Sie das folgende LGS, indem Sie es auf Diagonalenform bringen: Aufgabe 4.7 SoSe 2018Gegeben seien die folgenden Punkte Wir betrachten einen Würfel mit den Eckpunkten (a) Beschreiben Sie die Flächen dieses Würfels mittels Gleichungen vom Typ Aufgabe 4.8 SoSe 2018Wir drehen den Würfel aus Aufgabe 4.7 um die Aufgabe 4.9 SoSe 2018Wir drehen den gedrehten Würfel aus Aufgabe 4.8 um die Aufgabe 4.10 SoSe 2018Oberstudienrat Kramer gibt seiner 13a die drei Ebenen |
 drei Ebenen im
drei Ebenen im  , die genau den Punkt
, die genau den Punkt  gemeinsam haben.
gemeinsam haben.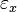 ist parallel zur
ist parallel zur 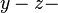 Ebene,
Ebene,
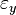 ist parallel zur
ist parallel zur 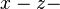 Ebene,
Ebene,
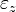 ist parallel zur
ist parallel zur 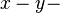 Ebene.
Ebene.
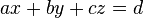 .
.
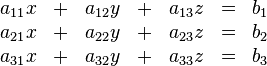
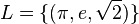 hat.
hat.
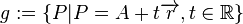 für
für 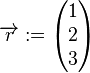 und
und 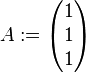 als Lösungsmenge eines Gleichungssystems vom Typ
als Lösungsmenge eines Gleichungssystems vom Typ 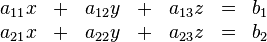 .
.
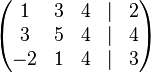
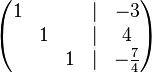
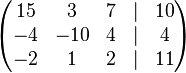
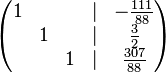
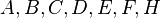 :
: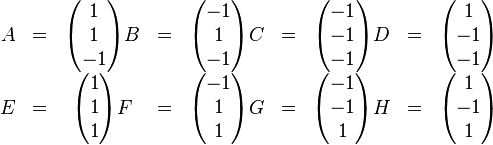
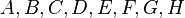 .
.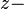 Achse mit einem Drehwinkel von
Achse mit einem Drehwinkel von 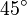 mathematisch positiv. Dabei werden die Eckpunkte unseres Würfels auf ihre Bilder
mathematisch positiv. Dabei werden die Eckpunkte unseres Würfels auf ihre Bilder 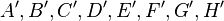 abgebildet.
abgebildet.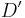 und nur die Koordinaten des Punktes
und nur die Koordinaten des Punktes 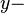 Achse mit einem Drehwinkel von
Achse mit einem Drehwinkel von 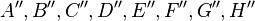 abgebildet.
Bestimmen Sie eine Gleichung der Form
abgebildet.
Bestimmen Sie eine Gleichung der Form 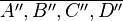 unseres Würfels.
unseres Würfels.
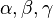 vor, wobei gelte
vor, wobei gelte 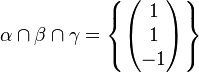 .
.