Übungsaufgaben zur Algebra, Serie 5 SoSe 2018: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 5.3) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 5.10) |
||
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 15: | Zeile 15: | ||
=Aufgabe 5.4= | =Aufgabe 5.4= | ||
| − | + | Beweisen Sie das Untergruppenkriterium 2. | |
=Aufgabe 5.5= | =Aufgabe 5.5= | ||
| − | + | Bestimmen Sie die zu <math>\begin{pmatrix} 0 & 1 \\ 1 & 1 \end{pmatrix} </math> inverse Matrix. | |
=Aufgabe 5.6= | =Aufgabe 5.6= | ||
| − | + | Bestimmen Sie die zu <math>\begin{pmatrix} 2 & 3 \\ 1 & 4 \end{pmatrix} </math> inverse Matrix. | |
=Aufgabe 5.7= | =Aufgabe 5.7= | ||
| + | Erstellen Sie einen Untergruppengraphen der Gruppe der Deckabbildungen des Quadrates. | ||
=Aufgabe 5.8= | =Aufgabe 5.8= | ||
| + | Beweisen Sie: Die Gruppe der durch <math>2</math> teilbaren ganzen Zahlen ist eine Untergruppe der Gruppe der ganzen Zahlen. | ||
=Aufgabe 5.9= | =Aufgabe 5.9= | ||
| − | + | Beweisen Sie: Die Menge der ungeraden ganzen Zahlen ist bezüglich der Addition keine Untergruppe der ganzen Zahlen. | |
=Aufgabe 5.10= | =Aufgabe 5.10= | ||
| − | + | Geben Sie zwei Matrizen an, die selbstinvers sind. | |
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Algebra]] | [[Kategorie:Algebra]] | ||
Aktuelle Version vom 3. Juni 2018, 15:04 Uhr
Aufgabe 5.1Es sei Aufgabe 5.2Es sei Aufgabe 5.3Beweisen Sie das Untergruppenkriterium 1. Aufgabe 5.4Beweisen Sie das Untergruppenkriterium 2. Aufgabe 5.5Bestimmen Sie die zu Aufgabe 5.6Bestimmen Sie die zu Aufgabe 5.7Erstellen Sie einen Untergruppengraphen der Gruppe der Deckabbildungen des Quadrates. Aufgabe 5.8Beweisen Sie: Die Gruppe der durch Aufgabe 5.9Beweisen Sie: Die Menge der ungeraden ganzen Zahlen ist bezüglich der Addition keine Untergruppe der ganzen Zahlen. Aufgabe 5.10Geben Sie zwei Matrizen an, die selbstinvers sind. |
![[G, \circ]](/images/math/4/6/8/4686bbf90bf7ebab892b288a31255920.png) eine Gruppe mit dem Einselement
eine Gruppe mit dem Einselement  . Beweisen Sie:
. Beweisen Sie: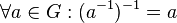 .
.
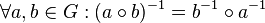 .
.
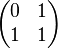 inverse Matrix.
inverse Matrix.
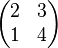 inverse Matrix.
inverse Matrix.
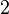 teilbaren ganzen Zahlen ist eine Untergruppe der Gruppe der ganzen Zahlen.
teilbaren ganzen Zahlen ist eine Untergruppe der Gruppe der ganzen Zahlen.

