SoSe 2018 Lösung von Aufgabe 6.03: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Kommentar --*m.g.* (Diskussion) 12:40, 11. Jun. 2018 (CEST)) |
|||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> | ||
| + | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| + | |||
| + | | valign="top" | | ||
| + | =Lösung 1= | ||
Halbraum EA- : Es sei Ebene E und ein Punkt A, welcher außerhalb von E liegt. Ein Punkt Q liegt ebenfalls außerhalb der Ebene E und auf der selben Seite der Ebene E wie der Punkt A. Der Halbraum EA- ist die Menge der Ebene und die Menge aller Punkte, die auf der selben Seite wie A und Q liegen. | Halbraum EA- : Es sei Ebene E und ein Punkt A, welcher außerhalb von E liegt. Ein Punkt Q liegt ebenfalls außerhalb der Ebene E und auf der selben Seite der Ebene E wie der Punkt A. Der Halbraum EA- ist die Menge der Ebene und die Menge aller Punkte, die auf der selben Seite wie A und Q liegen. | ||
Halbraum EA+ : | Halbraum EA+ : | ||
| + | ==Kommentar --[[Benutzer:*m.g.*|*m.g.*]] ([[Benutzer Diskussion:*m.g.*|Diskussion]]) 12:40, 11. Jun. 2018 (CEST)== | ||
| + | ===Einschätzung dieser Definition=== | ||
| + | |||
| + | Das ist eine informelle Definition. Was bedeutet mathematisch korrekt "Zwei Punkte liegen auf derselben Seite bezüglich einer Ebene"?<br /> | ||
| + | Vergleichen Sie mit der Definition der Halbebene. Hier ist der Trenner eine Gerade g. Was bedeutet, zwei Punkte liegen auf derselben Seite bezüglich der Geraden g? | ||
| + | |||
| + | ===Zur Sprache=== | ||
| + | ====Es sei ==== | ||
| + | Was soll das bedeuten: "Es sei Ebene E und ein Punkt A."?<br /> | ||
| + | Sie müssen den Unterschied der folgenden beiden Formulierungen erkennen, um sauber Definitionen zu schreiben: | ||
| + | # Es sei Ebene E und Punkt A, ... (nicht korrekt) | ||
| + | # Es sei E eine Ebene und A ein Punkt, der ... (korrekt) | ||
| + | ====Mengen==== | ||
| + | * Die Menge der Ebene E: Was ist das? Könnte als die folgende Menge S verstanden werden: <math>S:=\{E\}</math>, eine Menge, die als Element die Ebene hat. Wir brauchen aber die Menge die aus allen Punkten der Ebene besteht. | ||
| + | ====und==== | ||
| + | '''Und''' ist eine logische Verknüpfung zweier Aussagen. Die verknüpfung der beiden Ausagen a und b ist genau dann wahr, wenn a und b jeweils wahr sind. Schreibweise <math>a \land b</math>. Wir haben jedoch zwei Mengen, die "zu verknüpfen" wären. Die erste Menge ist E und die zweite Menge ist die Menge H aller Punkte, die mit A auf derselben Seite bezüglich E liegen. Diese beiden Mengen werden durch die Operation Vereinigungsmenge miteinander verknüpft. Schreibweise: <math>E \cup H</math>. | ||
| + | |||
| + | =Lösung 2= | ||
| + | |||
| + | =Lösung 3= | ||
| + | |||
| + | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
| + | |} | ||
| + | </div> | ||
| + | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 11. Juni 2018, 11:42 Uhr
Lösung 1Halbraum EA- : Es sei Ebene E und ein Punkt A, welcher außerhalb von E liegt. Ein Punkt Q liegt ebenfalls außerhalb der Ebene E und auf der selben Seite der Ebene E wie der Punkt A. Der Halbraum EA- ist die Menge der Ebene und die Menge aller Punkte, die auf der selben Seite wie A und Q liegen. Halbraum EA+ : Kommentar --*m.g.* (Diskussion) 12:40, 11. Jun. 2018 (CEST)Einschätzung dieser DefinitionDas ist eine informelle Definition. Was bedeutet mathematisch korrekt "Zwei Punkte liegen auf derselben Seite bezüglich einer Ebene"? Zur SpracheEs seiWas soll das bedeuten: "Es sei Ebene E und ein Punkt A."?
Mengen
undUnd ist eine logische Verknüpfung zweier Aussagen. Die verknüpfung der beiden Ausagen a und b ist genau dann wahr, wenn a und b jeweils wahr sind. Schreibweise Lösung 2Lösung 3 |
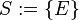 , eine Menge, die als Element die Ebene hat. Wir brauchen aber die Menge die aus allen Punkten der Ebene besteht.
, eine Menge, die als Element die Ebene hat. Wir brauchen aber die Menge die aus allen Punkten der Ebene besteht.
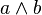 . Wir haben jedoch zwei Mengen, die "zu verknüpfen" wären. Die erste Menge ist E und die zweite Menge ist die Menge H aller Punkte, die mit A auf derselben Seite bezüglich E liegen. Diese beiden Mengen werden durch die Operation Vereinigungsmenge miteinander verknüpft. Schreibweise:
. Wir haben jedoch zwei Mengen, die "zu verknüpfen" wären. Die erste Menge ist E und die zweite Menge ist die Menge H aller Punkte, die mit A auf derselben Seite bezüglich E liegen. Diese beiden Mengen werden durch die Operation Vereinigungsmenge miteinander verknüpft. Schreibweise: 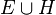 .
.

