SoSe 2018 Lösung von Aufgabe 6.01: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Beweis 1) |
*m.g.* (Diskussion | Beiträge) (→Kommentar --*m.g.* (Diskussion) 16:32, 10. Jun. 2018 (CEST)) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 16: | Zeile 16: | ||
Strecke AB ist größer als Strecke AP | Strecke AB ist größer als Strecke AP | ||
==Kommentar --[[Benutzer:*m.g.*|*m.g.*]] ([[Benutzer Diskussion:*m.g.*|Diskussion]]) 16:32, 10. Jun. 2018 (CEST)== | ==Kommentar --[[Benutzer:*m.g.*|*m.g.*]] ([[Benutzer Diskussion:*m.g.*|Diskussion]]) 16:32, 10. Jun. 2018 (CEST)== | ||
| − | Hier ist Luft nach oben. | + | Hier ist Luft nach oben (freundlich ausgedrückt). |
Natürlich können wir beide Implikationen zusammenfassen zu einer Äquivalenz. Def Ü genau dann, wenn Def V. | Natürlich können wir beide Implikationen zusammenfassen zu einer Äquivalenz. Def Ü genau dann, wenn Def V. | ||
Dazu sind zwei Beweise zu führen. | Dazu sind zwei Beweise zu führen. | ||
| Zeile 41: | Zeile 41: | ||
Wenn Fall 1 eintritt folgt Fall a.<br /> | Wenn Fall 1 eintritt folgt Fall a.<br /> | ||
Es bleibt zu zeigen: <br /> | Es bleibt zu zeigen: <br /> | ||
| − | <math>P \in AB \land \vert AP\vert > \vert BP\vert \Rightarrow \operatorname{Zw}(A,B,P) </math> | + | <math>P \in AB \land \vert AP\vert > \vert BP\vert \Rightarrow \operatorname{Zw}(A,B,P) </math><br /> |
| + | Ferner dürfen wir für diesen Beweis voraussetzen, dass <math>P \not \in \overline{AB}</math>, denn Fall 1 wurde schon abgearbeitet.<br /> | ||
| + | Von drei paarweise verschiedenen Punkten <math>A, B, P</math> liegt genau einer zwischen den beiden anderen (in der Vorlesung bewiesen).<br /> | ||
| + | Prinzipiell könnte also gelten:<br /> | ||
| + | <math> | ||
| + | \begin{matrix} | ||
| + | \text{I} & \operatorname{Zw}(APB) \\ | ||
| + | \text{II} & \operatorname{Zw}(PAB) \\ | ||
| + | \text{III} & \operatorname{Zw}(ABP) \\ | ||
| + | \end{matrix} | ||
| + | </math> | ||
| + | |||
| + | <math>\text{I}</math> kann nicht eintreten, denn das wäre Fall 1 und der ist schon abgearbeitet. ... den Rest können Sie alleine. | ||
| + | ===Beweis 2=== | ||
| + | Wenn <math>P</math> anch Def V zu <math>AB^+</math> gehört, dann gehört <math>P</math> auch nach Def Ü zu <math>AB^+</math>. ... | ||
| + | =Lösung 2= | ||
| + | Probieren Sie beide Beweise korrekt zu führen. | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Einführung_S]] | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 10. Juni 2018, 15:59 Uhr
Aufgabe 6.01In einer Übung definierte eine Kommilitonin den Begriff Halbgerade
Lösung 1Behauptung: Def V <=> Def Ü zz. P Element von AB, d.h. P muss zwischen den Punkten A und B liegen Strecke AB ist größer als Strecke AP Kommentar --*m.g.* (Diskussion) 16:32, 10. Jun. 2018 (CEST)Hier ist Luft nach oben (freundlich ausgedrückt). Natürlich können wir beide Implikationen zusammenfassen zu einer Äquivalenz. Def Ü genau dann, wenn Def V. Dazu sind zwei Beweise zu führen. Beweis 1Wenn VoraussetzungIn diesem Fall gilt: Anders ausgedrückt: Fall 1
Fall 2
Behauptung
Fall a
Fall b
Der BeweisWenn Fall 1 eintritt folgt Fall a.
Beweis 2Wenn Lösung 2Probieren Sie beide Beweise korrekt zu führen. |
 wie folgt:
wie folgt: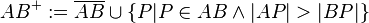
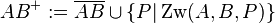 Beweisen Sie:
Beweisen Sie:
 Definition Ü
Definition Ü
 ein Punkt des Strahls
ein Punkt des Strahls  oder es gilt
oder es gilt 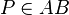 und
und 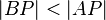 .
.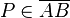
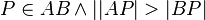
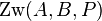
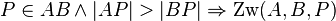
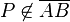 , denn Fall 1 wurde schon abgearbeitet.
, denn Fall 1 wurde schon abgearbeitet.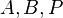 liegt genau einer zwischen den beiden anderen (in der Vorlesung bewiesen).
liegt genau einer zwischen den beiden anderen (in der Vorlesung bewiesen).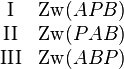
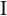 kann nicht eintreten, denn das wäre Fall 1 und der ist schon abgearbeitet. ... den Rest können Sie alleine.
kann nicht eintreten, denn das wäre Fall 1 und der ist schon abgearbeitet. ... den Rest können Sie alleine.

