Diskussion:Lösung von Aufgabe 10.4: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
 
Zeile 3: Zeile 3:
 
'''Antwort 1''' <br />Soweit ich es in Erinnerung habe, war das der Fall, dass die Winkelhalbierende nicht in der selben Ebene wie die beschriebenen Strahlen liegt.<br /><br />Hier nochmal die Definition aus dem Skript: (Verlinken hat nicht geklappt, desshalb hab ich sie per copy&paste eingefügt)<br />"Definition VI.2<br />  
 
'''Antwort 1''' <br />Soweit ich es in Erinnerung habe, war das der Fall, dass die Winkelhalbierende nicht in der selben Ebene wie die beschriebenen Strahlen liegt.<br /><br />Hier nochmal die Definition aus dem Skript: (Verlinken hat nicht geklappt, desshalb hab ich sie per copy&paste eingefügt)<br />"Definition VI.2<br />  
 
Es seien <math>\ p</math>,<math>\ w</math> und <math>\ q</math> drei Halbgeraden ein und derselben Ebene mit dem gemeinsamen Anfangspunkt <math>\ S</math>. Die Halbgerade <math>\ w</math> ist die Winkelhalbierende des Winkels <math>\angle pq</math>, wenn <math>\ w</math> im Inneren von  <math>\angle pq</math> liegt und die beiden Winkel <math>\angle pw</math> und <math>\angle wq</math> dieselbe Größe haben."<br /><br />und im Vergleich dazu die Definition aus der Aufgabe:<br />"Die Halbgerade <math>\ SW^+</math> ist die Winkelhalbierende des Winkels <math>\angle ASB</math>, wenn <math>| \angle ASW| = | \angle WSB |</math>."<br /> --[[Benutzer:Farina|Farina]] 06:34, 16. Jul. 2010 (UTC)
 
Es seien <math>\ p</math>,<math>\ w</math> und <math>\ q</math> drei Halbgeraden ein und derselben Ebene mit dem gemeinsamen Anfangspunkt <math>\ S</math>. Die Halbgerade <math>\ w</math> ist die Winkelhalbierende des Winkels <math>\angle pq</math>, wenn <math>\ w</math> im Inneren von  <math>\angle pq</math> liegt und die beiden Winkel <math>\angle pw</math> und <math>\angle wq</math> dieselbe Größe haben."<br /><br />und im Vergleich dazu die Definition aus der Aufgabe:<br />"Die Halbgerade <math>\ SW^+</math> ist die Winkelhalbierende des Winkels <math>\angle ASB</math>, wenn <math>| \angle ASW| = | \angle WSB |</math>."<br /> --[[Benutzer:Farina|Farina]] 06:34, 16. Jul. 2010 (UTC)
 +
 +
[[Category:Einführung_Geometrie]]

Aktuelle Version vom 16. November 2010, 22:22 Uhr

Es gab einen zweiten Fall, für den die angegebene Definition nicht korrekt ist. Dieser wurde in der Übung besprochen, leider hab ich es nicht ganz verstanden. Weiß jemand vielleicht, welcher Fall dieser war?

Antwort 1
Soweit ich es in Erinnerung habe, war das der Fall, dass die Winkelhalbierende nicht in der selben Ebene wie die beschriebenen Strahlen liegt.

Hier nochmal die Definition aus dem Skript: (Verlinken hat nicht geklappt, desshalb hab ich sie per copy&paste eingefügt)
"Definition VI.2
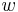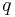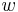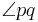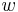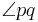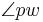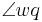Es seien \ p,\ w und \ q drei Halbgeraden ein und derselben Ebene mit dem gemeinsamen Anfangspunkt \ S. Die Halbgerade \ w ist die Winkelhalbierende des Winkels \angle pq, wenn \ w im Inneren von \angle pq liegt und die beiden Winkel \angle pw und \angle wq dieselbe Größe haben."

und im Vergleich dazu die Definition aus der Aufgabe:
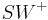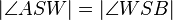"Die Halbgerade \ SW^+ ist die Winkelhalbierende des Winkels \angle ASB, wenn | \angle ASW| = | \angle WSB |."
--Farina 06:34, 16. Jul. 2010 (UTC)

Von „http://geometrie.zum.de/index.php?title=Diskussion:Lösung_von_Aufgabe_10.4&oldid=4937“