Lösung von Aufg. 7.3P (WS 18 19): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Gegeben seien drei paarweise verschiedene und '''kollineare''' Punkte ''A'', ''B'' und ''C'' in einer Ebene ''E''. Ferner sei eine Gerade ''g'' Teilmenge der E…“)
 
 
Zeile 3: Zeile 3:
 
(Hinweis: Nehmen Sie einen weiteren Punkt D an, mit <math>\overline{AD}\cap g\not=\lbrace \rbrace  </math> und nutzen Sie den Satz von Pasch)<br />
 
(Hinweis: Nehmen Sie einen weiteren Punkt D an, mit <math>\overline{AD}\cap g\not=\lbrace \rbrace  </math> und nutzen Sie den Satz von Pasch)<br />
  
 +
 +
Die Punkte A, B, D bilden das Dreieck <math>\overline{ABD}</math>, <math>\overline{AB}</math> wird von g nicht geschnitten, <math>\overline{AD}</math> wird geschnitten. '''- Voraussetzung, Hinweis'''<br />
 +
=> g muss noch eine weitere Seite von <math>\overline{ABD}</math> schneiden, also <math>\overline{BD}</math>. '''- 1., Satz von Pasch'''<br />
 +
=> B, C, D bilden ein Dreieck <math>\overline{BCD}</math>, g schneidet <math>\overline{BD}</math> und genau eine weitere Seite. '''- Satz von Pasch'''<br />
 +
=> g schneidet <math>\overline{CD}</math>, da g <math>\overline{BC}</math> nicht schneidet. '''- 3., Vorraussetzung'''<br />
 +
=> A, C, D bilden das Dreieck <math>\overline{ACD}</math>, g schneidet <math>\overline{AD}</math> und <math>\overline{CB}</math>, somit kann g <math>\overline{AC}</math> nicht schneiden. '''- 1., 4., Satz von Pasch'''--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 15:24, 30. Nov. 2018 (CET)
  
 
[[Kategorie:Geo_P]]
 
[[Kategorie:Geo_P]]

Aktuelle Version vom 30. November 2018, 15:24 Uhr

Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:

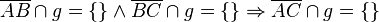
\overline{AB}\cap g=\lbrace \rbrace \wedge \overline{BC}\cap g=\lbrace \rbrace\Rightarrow \overline{AC}\cap g=\lbrace \rbrace

(Hinweis: Nehmen Sie einen weiteren Punkt D an, mit 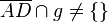\overline{AD}\cap g\not=\lbrace \rbrace und nutzen Sie den Satz von Pasch)


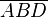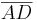Die Punkte A, B, D bilden das Dreieck \overline{ABD}, \overline{AB} wird von g nicht geschnitten, \overline{AD} wird geschnitten. - Voraussetzung, Hinweis
=> g muss noch eine weitere Seite von 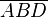\overline{ABD} schneiden, also 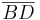\overline{BD}. - 1., Satz von Pasch
=> B, C, D bilden ein Dreieck 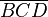\overline{BCD}, g schneidet 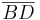\overline{BD} und genau eine weitere Seite. - Satz von Pasch
=> g schneidet \overline{CD}, da g \overline{BC} nicht schneidet. - 3., Vorraussetzung
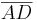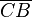=> A, C, D bilden das Dreieck \overline{ACD}, g schneidet \overline{AD} und \overline{CB}, somit kann g \overline{AC} nicht schneiden. - 1., 4., Satz von Pasch--CIG UA (Diskussion) 15:24, 30. Nov. 2018 (CET)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._7.3P_(WS_18_19)&oldid=32581“