Lösung von Aufg. 6.5P (WS 18 19): Unterschied zwischen den Versionen
| (4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 16: | Zeile 16: | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Ich habe den Beweis leider nicht in Tabellenform hinbekommen. | Ich habe den Beweis leider nicht in Tabellenform hinbekommen. | ||
| − | Voraussetzung: g schneidet eine Seite des Dreiecks ABC. | + | Voraussetzung: g schneidet eine Seite des Dreiecks ABC.<br /> |
Behauptung: g schneidet genau eine weitere Seite des Dreiecks ABC. | Behauptung: g schneidet genau eine weitere Seite des Dreiecks ABC. | ||
Beispiel: | Beispiel: | ||
| − | Voraussetzung: g schneidet Seite AB. | + | Voraussetzung: g schneidet Seite AB.<br /> |
| + | |||
Behauptung: g schneidet entweder Seite AC oder Seite BC. | Behauptung: g schneidet entweder Seite AC oder Seite BC. | ||
| − | Punkt A teilt die Ebene E in zwei Halbebenen gA+ und gA-. | + | |
| − | Gerade g schneidet die Seite AB (Voraussetzung). | + | Punkt A teilt die Ebene E in zwei Halbebenen gA+ und gA-. Gerade g schneidet die Seite AB (Voraussetzung). |
| + | etwas genauer wäre an dieser Stelle: g teilt die Ebene E bezüglich des Punktes A in genau zwei Halbebenen (Begründung: Ebenenteilungsaxiom)--[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 13:44, 29. Nov. 2018 (CET) | ||
Somit muss die Gerade g entweder die Seite AC oder die Seite BC schneiden (Behauptung). | Somit muss die Gerade g entweder die Seite AC oder die Seite BC schneiden (Behauptung). | ||
Es gibt einen Punkt C, der auf der selben Ebene (wie Punkt A und Punkt B) liegen. Somit kann Punkt C entweder in der Halbebene gA+ oder in der Halbebene gA- liegen. | Es gibt einen Punkt C, der auf der selben Ebene (wie Punkt A und Punkt B) liegen. Somit kann Punkt C entweder in der Halbebene gA+ oder in der Halbebene gA- liegen. | ||
| − | + | ||
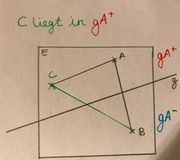
| + | Liegt Punkt C in der Halbebene gA+, dann schneidet die Gerade g laut der Definition der Halbebene die Seite BC, aber nicht die Seite AC. (siehe Zeichnung) | ||
| + | [[Datei:GA+.jpg|thumb|Beweis Satz von Pasch]] | ||
| + | |||
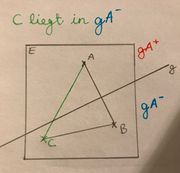
| + | Liegt Punkt C in der Halbebene gA-, dann schneidet die Gerade g laut der Definition der Halbebene die Seite AC, aber nicht die Seite BC. (siehe Zeichnung) | ||
| + | [[Datei:GA-.jpg|thumb|Beweis Satz von Pasch]] | ||
| − | + | (Das Gleiche gilt, wenn man statt Seite AB die Seite AC oder die Seite BC als Voraussetzung nutzt.) | |
| + | --[[Benutzer:Student01|Student01]] ([[Benutzer Diskussion:Student01|Diskussion]]) 17:14, 21. Nov. 2018 (CET) | ||
| − | ( | + | 1. G schneidet <math>\overline{AB}</math> im Punk P mit P= Zw.(A,P,B). '''- Voraussetzung'''<br /> |
| + | 2. Es gibt einen Punk G1 auf G, der in der Halbebene <math>ABC^-</math> liegt.<br /> | ||
| + | g ist die Summe der beiden Halbgeraden <math>PG1^+</math> und <math>PG1^-</math> (und P) '''- Logik, 1'''<br /> | ||
| + | 3. <math>PG1^-</math> ist gleich der Halbgeraden <math>PG2^+</math> mit G2 Element g und Element <math>ABC^+</math>'''- Logik, 2'''<br /> | ||
| + | 4.<math>PG2^+</math> ist Element von <math>\overline{AB}C^+</math>, genauso wie <math>\overline{AC}</math> und <math>\overline{BC}</math>'''- Logik, 3'''<br /> | ||
| + | das kann nicht sein, da Widerspruch zum Satz von Pasch --[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 13:44, 29. Nov. 2018 (CET) | ||
| + | 5. <math>PG2^+</math> schneidet C nicht, aber schneidet einen Punkt F, der den gleichen Abstand zur Geraden AB hat. '''- Voraussetzung, Logik'''<br /> | ||
| + | 6. <math>PG2^+</math> schneidet entweder <math>\overline{AC}</math> (wenn F links von C) oder <math>\overline{BC}</math> (wenn F rechts von C)'''- Logik, 4, 5'''<br />--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 13:40, 23. Nov. 2018 (CET) | ||
| + | dieser Beweis ist so leider nicht zielführend --[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 13:44, 29. Nov. 2018 (CET) | ||
Aktuelle Version vom 29. November 2018, 13:44 Uhr
Beweisen Sie den Satz von Pasch.
Voraussetzung: g schneidet eine Seite des Dreiecks ABC
Behauptung: g schneidet genau eine weitere Seite des Dreiecks ABC
| Beweisschritt | Begründung |
|---|---|
| 1. g schneidet eine Seite des Dreiecks ABC | Voraussetzung |
| 2. g hat keinen Anfangs und Endpunkt | Def (Gerade) |
| 3. g muss eine weitere Seite des Dreiecks schneiden | Logik, 2. |
anschaulich plausibel aber kein Beweis. Versuchen Sie ohne Anschauung zu argumentieren--Schnirch (Diskussion) 12:12, 21. Nov. 2018 (CET)
Ich habe den Beweis leider nicht in Tabellenform hinbekommen.
Voraussetzung: g schneidet eine Seite des Dreiecks ABC.
Behauptung: g schneidet genau eine weitere Seite des Dreiecks ABC.
Beispiel:
Voraussetzung: g schneidet Seite AB.
Behauptung: g schneidet entweder Seite AC oder Seite BC.
Punkt A teilt die Ebene E in zwei Halbebenen gA+ und gA-. Gerade g schneidet die Seite AB (Voraussetzung).
etwas genauer wäre an dieser Stelle: g teilt die Ebene E bezüglich des Punktes A in genau zwei Halbebenen (Begründung: Ebenenteilungsaxiom)--Schnirch (Diskussion) 13:44, 29. Nov. 2018 (CET)
Somit muss die Gerade g entweder die Seite AC oder die Seite BC schneiden (Behauptung).
Es gibt einen Punkt C, der auf der selben Ebene (wie Punkt A und Punkt B) liegen. Somit kann Punkt C entweder in der Halbebene gA+ oder in der Halbebene gA- liegen.
Liegt Punkt C in der Halbebene gA+, dann schneidet die Gerade g laut der Definition der Halbebene die Seite BC, aber nicht die Seite AC. (siehe Zeichnung)
Liegt Punkt C in der Halbebene gA-, dann schneidet die Gerade g laut der Definition der Halbebene die Seite AC, aber nicht die Seite BC. (siehe Zeichnung)
(Das Gleiche gilt, wenn man statt Seite AB die Seite AC oder die Seite BC als Voraussetzung nutzt.)
--Student01 (Diskussion) 17:14, 21. Nov. 2018 (CET)
1. G schneidet  im Punk P mit P= Zw.(A,P,B). - Voraussetzung
im Punk P mit P= Zw.(A,P,B). - Voraussetzung
2. Es gibt einen Punk G1 auf G, der in der Halbebene 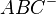 liegt.
liegt.
g ist die Summe der beiden Halbgeraden 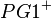 und
und 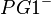 (und P) - Logik, 1
(und P) - Logik, 1
3. 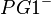 ist gleich der Halbgeraden
ist gleich der Halbgeraden 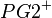 mit G2 Element g und Element
mit G2 Element g und Element 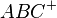 - Logik, 2
- Logik, 2
4.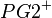 ist Element von
ist Element von 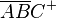 , genauso wie
, genauso wie  und
und  - Logik, 3
- Logik, 3
das kann nicht sein, da Widerspruch zum Satz von Pasch --Schnirch (Diskussion) 13:44, 29. Nov. 2018 (CET)
5. 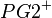 schneidet C nicht, aber schneidet einen Punkt F, der den gleichen Abstand zur Geraden AB hat. - Voraussetzung, Logik
schneidet C nicht, aber schneidet einen Punkt F, der den gleichen Abstand zur Geraden AB hat. - Voraussetzung, Logik
6. 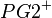 schneidet entweder
schneidet entweder  (wenn F links von C) oder
(wenn F links von C) oder  (wenn F rechts von C)- Logik, 4, 5
(wenn F rechts von C)- Logik, 4, 5
--CIG UA (Diskussion) 13:40, 23. Nov. 2018 (CET)
dieser Beweis ist so leider nicht zielführend --Schnirch (Diskussion) 13:44, 29. Nov. 2018 (CET)