Lösung von Aufg. 6.3P (WS 18 19): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
CIG UA (Diskussion | Beiträge) |
|||
| Zeile 3: | Zeile 3: | ||
1. M <span>∩</span> N = O, mit M, N, O sind konvex<br /> | 1. M <span>∩</span> N = O, mit M, N, O sind konvex<br /> | ||
| + | dass O konvex ist sollen Sie ja erst noch beweisen und deshalb nicht schon oben als gegeben annehmen.--[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 13:23, 29. Nov. 2018 (CET) | ||
2. {A,B | <math>\overline{AB}</math> ε M} <span>∩</span> {C,D | <math>\overline{CD}</math> ε N} <=> O<br /> | 2. {A,B | <math>\overline{AB}</math> ε M} <span>∩</span> {C,D | <math>\overline{CD}</math> ε N} <=> O<br /> | ||
3. O = {A,B,C,D | <math>\overline{AB}</math> ε M <math>\wedge</math> <math>\overline{AB}</math> ε N <math>\wedge</math> <math>\overline{CD}</math> ε M <math>\wedge</math> <math>\overline{CD}</math> ε N}<br /> | 3. O = {A,B,C,D | <math>\overline{AB}</math> ε M <math>\wedge</math> <math>\overline{AB}</math> ε N <math>\wedge</math> <math>\overline{CD}</math> ε M <math>\wedge</math> <math>\overline{CD}</math> ε N}<br /> | ||
Aktuelle Version vom 29. November 2018, 13:23 Uhr
Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex.
1. M ∩ N = O, mit M, N, O sind konvex
dass O konvex ist sollen Sie ja erst noch beweisen und deshalb nicht schon oben als gegeben annehmen.--Schnirch (Diskussion) 13:23, 29. Nov. 2018 (CET)
2. {A,B |  ε M} ∩ {C,D |
ε M} ∩ {C,D |  ε N} <=> O
ε N} <=> O
3. O = {A,B,C,D |  ε M
ε M 
 ε N
ε N 
 ε M
ε M 
 ε N}
ε N}
4. O = {A,B,C,D | 



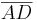



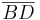

 ε O}
ε O}
5. O ist konvex.
Begründung von Schritt 4 -> Transitivität der Korrelation "kongruente (Schnitt)menge" --CIG UA (Diskussion) 12:52, 23. Nov. 2018 (CET)

