Lösung von Aufgabe 8.3P (WS 18 19): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Azalea (Diskussion | Beiträge) |
CIG UA (Diskussion | Beiträge) |
||
| (4 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
<ggb_applet width="754" height="535" version="4.0" ggbBase64="UEsDBBQACAAIAFeAxkAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAFeAxkAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VlZb9s4EH5uf8VAz7Et6rJd2C3aAmlTpAeQ7GKxb5REy2wkUSvSV9Efv0NSkmUnaZv0QFojCUlxOMc3B0fO7Nm2yGHNaslFOXfI0HWAlYlIeZnNnZVaDCbOs6ePZxkTGYtrCgtRF1TNnUBT8nTuLCiLGU3DAfUXwSBgfjyYLpLxIGaeO6EuiZk/dQC2kj8pxTtaMFnRhF0kS1bQc5FQZQQvlaqejEabzWbYihqKOhtlWTzcytQBVLOUc6eZPEF2B4c2viH3XJeM/nl7btkPeCkVLRPmgDZhxZ8+fjTb8DIVG9jwVC3nzjjyHFgyni3RpnA6dmCkiSoEpGKJ4msm8WhvaWxWReUYMlrq/Ud2BnlnjgMpX/OU1XPHHfpHHwdEzVmpGlrSyBy13GZrzjaWrZ4ZiYEDSog8ppojfP4Mnuu5cKIHYgcPhyiyW6595vp28OwQ2CG0NIE9HljSwNIEliZAHddc8jhn2sG5RAR5uajRe91aql3OjD7Ng7315ARtkvwTEqM8ByzkqPiJexK45tfa3DOQ9CSqenVHga24cRh8mzjvuwz0O/OO5Xm3mRd9QaC191vsI2EPztA9MT/m95pE/0smHku06+8TGAW/xMTZqE2PWZMRIJeatokaxQqpc8SfQjjVoU4gxHyIxhjZIZApDmMPMAOAhBCEuCQTiPQ4Bn+MGwH4MAFNR3wwCRFO8E8wNswiCJGZfjrGPASCggIIfSAmjwLA7AGTi5iXno8UYQghHtLiiadZ+BEEEa78CQSoo07DMUFCHw/iGsV74BPw9WEyBi+CSPMjgU7vaKJVR5YeRC5ERDPETMYsthmM9BPwtTVRAxcvq5U6gCgp0naqRNX5AqmxBu0rna1JB4Xw0SynMcvxbrjQngRY01xngxG0EKWC1omefZbVtFryRF4wpfCUhI90Tc+pYttTpJatbEObiFJ+qIV6KfJVUUqARORup7PISW/udVrjwu9tBP2NsLcR9ebjG+UK3IGVZChf1LIlp2l6pin2ZQGRfF/muxc1o1eV4IdmzEbmmpmxVZLzlNPybwxWLUXjAt2to8tGe+sEftAqIur0YicxgmH7L6sF7kXD6cHHgV2zQ/zh0Y5MqE690B26/c8kxEPNXjA9PDSxktm6cxDdsr2tWc27UNHzM/lC5Gm3bax/SSu1qk27gDlca5uel1nOTISYQot3cXIVi+2FDQ3f8rrcVbhyrQJxZlCHWpdU1DdrxtiOhkZr1lHpYpPZITZDE2487UjI1DM0ZoztaKgwfq12jbGkNZS4rSQuTUlznSZx2nKlo1/f7quSq/N2oXhy1VhL7IF3qyJmXQwd8iQ/iudsdBRksytWlyxvYhrduRIraVO0F+4pS3iBS7vRQEK1x/5CBezTlGU1axXPTTdmATO7bj9crz02rE5rUZyV60sMhyMFZqNWy5lMal7pqIMY74Ertg+slEuK10jaP6eTEE1P9HWB8CgNDabnSi1FbRourCo4GsqioGUKpbl5zkqFsGEJc/bVkGJd2T5HjyADLCs7MzXai5VqCU6tug03ndM5K7BtA2Ui1wR/575Tw137CUT8EaV1d6rd7zkA928PY6B5taS6a2zgzOmO1QcAG45vRXqDNyRs7VHYzZ2BmXyyTb3tarXKOgsP6rZ9euRHDC5r7TU8Pxi7b8LyGMBXdwHw1f0AJJ6tFmZsqsW9MaQlZoaJL6zBlc28ijGbtFZpnFTIzpS7gzukRZ+08P8o9L8E2uv7geYayNwHBlj0y8L15nx/c5dwffOHhOvPBj/fZaI8gv+NrbqvcfB04gP1m2p74A+81HJsHIilTi11YqljHLDVo19zmRXfOqXjeNgFKOxQr/DVW5puRTV9iZm85mnKzNvJ6H7+Dn3j75AYd7s9Z5O7OPv2giBZpledIuk9A/N2Rb/7IiJtKRxEe273QJ/9V9oj0jZGvKhynnDVRU6uA7277zExrnc/V4xVuvN8X17WtJT62yxL0+uqvhHp5OEgHR3dOX8W0PHDAbrrrfYx/SchTR8O0oPjmP6dcT7sHZ5/BeX9S+ODbdrGwyiytX3oeT+9zX3x+wMWDl0LWDAMgh8C2Kj/Qmy+eGr+b/L0f1BLBwi3MQj2KwYAANQZAABQSwECFAAUAAgACABXgMZA1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAFeAxkC3MQj2KwYAANQZAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAwgYAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br /><br /> | <ggb_applet width="754" height="535" version="4.0" ggbBase64="UEsDBBQACAAIAFeAxkAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAFeAxkAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VlZb9s4EH5uf8VAz7Et6rJd2C3aAmlTpAeQ7GKxb5REy2wkUSvSV9Efv0NSkmUnaZv0QFojCUlxOMc3B0fO7Nm2yGHNaslFOXfI0HWAlYlIeZnNnZVaDCbOs6ePZxkTGYtrCgtRF1TNnUBT8nTuLCiLGU3DAfUXwSBgfjyYLpLxIGaeO6EuiZk/dQC2kj8pxTtaMFnRhF0kS1bQc5FQZQQvlaqejEabzWbYihqKOhtlWTzcytQBVLOUc6eZPEF2B4c2viH3XJeM/nl7btkPeCkVLRPmgDZhxZ8+fjTb8DIVG9jwVC3nzjjyHFgyni3RpnA6dmCkiSoEpGKJ4msm8WhvaWxWReUYMlrq/Ud2BnlnjgMpX/OU1XPHHfpHHwdEzVmpGlrSyBy13GZrzjaWrZ4ZiYEDSog8ppojfP4Mnuu5cKIHYgcPhyiyW6595vp28OwQ2CG0NIE9HljSwNIEliZAHddc8jhn2sG5RAR5uajRe91aql3OjD7Ng7315ARtkvwTEqM8ByzkqPiJexK45tfa3DOQ9CSqenVHga24cRh8mzjvuwz0O/OO5Xm3mRd9QaC191vsI2EPztA9MT/m95pE/0smHku06+8TGAW/xMTZqE2PWZMRIJeatokaxQqpc8SfQjjVoU4gxHyIxhjZIZApDmMPMAOAhBCEuCQTiPQ4Bn+MGwH4MAFNR3wwCRFO8E8wNswiCJGZfjrGPASCggIIfSAmjwLA7AGTi5iXno8UYQghHtLiiadZ+BEEEa78CQSoo07DMUFCHw/iGsV74BPw9WEyBi+CSPMjgU7vaKJVR5YeRC5ERDPETMYsthmM9BPwtTVRAxcvq5U6gCgp0naqRNX5AqmxBu0rna1JB4Xw0SynMcvxbrjQngRY01xngxG0EKWC1omefZbVtFryRF4wpfCUhI90Tc+pYttTpJatbEObiFJ+qIV6KfJVUUqARORup7PISW/udVrjwu9tBP2NsLcR9ebjG+UK3IGVZChf1LIlp2l6pin2ZQGRfF/muxc1o1eV4IdmzEbmmpmxVZLzlNPybwxWLUXjAt2to8tGe+sEftAqIur0YicxgmH7L6sF7kXD6cHHgV2zQ/zh0Y5MqE690B26/c8kxEPNXjA9PDSxktm6cxDdsr2tWc27UNHzM/lC5Gm3bax/SSu1qk27gDlca5uel1nOTISYQot3cXIVi+2FDQ3f8rrcVbhyrQJxZlCHWpdU1DdrxtiOhkZr1lHpYpPZITZDE2487UjI1DM0ZoztaKgwfq12jbGkNZS4rSQuTUlznSZx2nKlo1/f7quSq/N2oXhy1VhL7IF3qyJmXQwd8iQ/iudsdBRksytWlyxvYhrduRIraVO0F+4pS3iBS7vRQEK1x/5CBezTlGU1axXPTTdmATO7bj9crz02rE5rUZyV60sMhyMFZqNWy5lMal7pqIMY74Ertg+slEuK10jaP6eTEE1P9HWB8CgNDabnSi1FbRourCo4GsqioGUKpbl5zkqFsGEJc/bVkGJd2T5HjyADLCs7MzXai5VqCU6tug03ndM5K7BtA2Ui1wR/575Tw137CUT8EaV1d6rd7zkA928PY6B5taS6a2zgzOmO1QcAG45vRXqDNyRs7VHYzZ2BmXyyTb3tarXKOgsP6rZ9euRHDC5r7TU8Pxi7b8LyGMBXdwHw1f0AJJ6tFmZsqsW9MaQlZoaJL6zBlc28ijGbtFZpnFTIzpS7gzukRZ+08P8o9L8E2uv7geYayNwHBlj0y8L15nx/c5dwffOHhOvPBj/fZaI8gv+NrbqvcfB04gP1m2p74A+81HJsHIilTi11YqljHLDVo19zmRXfOqXjeNgFKOxQr/DVW5puRTV9iZm85mnKzNvJ6H7+Dn3j75AYd7s9Z5O7OPv2giBZpledIuk9A/N2Rb/7IiJtKRxEe273QJ/9V9oj0jZGvKhynnDVRU6uA7277zExrnc/V4xVuvN8X17WtJT62yxL0+uqvhHp5OEgHR3dOX8W0PHDAbrrrfYx/SchTR8O0oPjmP6dcT7sHZ5/BeX9S+ODbdrGwyiytX3oeT+9zX3x+wMWDl0LWDAMgh8C2Kj/Qmy+eGr+b/L0f1BLBwi3MQj2KwYAANQZAABQSwECFAAUAAgACABXgMZA1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAFeAxkC3MQj2KwYAANQZAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAwgYAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br /><br /> | ||
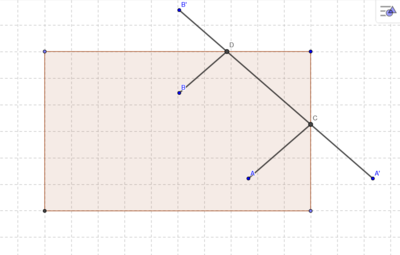
| − | [[Datei:Lösung von Aufgabe 8 3P (WS 18 19) – Geometrie-Wiki.png|400px]] Betrag(Strecke AB) ist der kürzeste Weg von A über Bande (rechts) und Bande (oben) zu B. Def (Strecke)-[[Benutzer:Azalea|Azalea]] ([[Benutzer Diskussion:Azalea|Diskussion]]) 18:22, 6. Dez. 2018 (CET) | + | [[Datei:Lösung von Aufgabe 8 3P (WS 18 19) – Geometrie-Wiki.png|400px]] <br /> |
| + | Betrag(Strecke AB) ist der kürzeste Weg von A über Bande (rechts) und Bande (oben) zu B. Def (Strecke)-[[Benutzer:Azalea|Azalea]] ([[Benutzer Diskussion:Azalea|Diskussion]]) 18:22, 6. Dez. 2018 (CET) | ||
| + | <br /> | ||
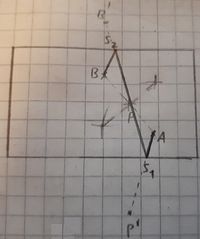
| + | [[Datei:Aufgabe 8.3.jpg|200px]]<br /> | ||
| + | 1. Mittelpunkt von <math>\overline{AB}</math> konstruieren.<br /> | ||
| + | 2. P an der Unterkante spiegeln, B an der Oberkante spiegeln.<br /> | ||
| + | 3. <math>\overline{AP'}</math> konstruieren, mit dem Schnittpunkt S1 <math>\overline{S1B'}</math> konstruieren, abschließend <math>\overline{S2B'}</math>.--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 11:30, 7. Dez. 2018 (CET) | ||
| + | |||
| + | auch eine schöne Lösung! -Erklärung?--[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 11:58, 10. Dez. 2018 (CET) | ||
| + | |||
| + | Da A und B den gleichen Abstand zu P haben ist die Verbindung jeweils eines Punktes zu P (die kürzeste über die jeweilige Bande) auch gleichzeitig vom Betrag und von den Winkeln gleich der anderen. Bzw: Wenn wir P als Spiegelpunkt nehmen, dann wird A-S1-P auf P-S2-B abgebildet und andersherum.--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 11:14, 14. Dez. 2018 (CET) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Aktuelle Version vom 14. Dezember 2018, 11:14 Uhr
Die nachfolgende GeoGebra-Applikation zeigt einen Billardtisch mit zwei Kugeln in der Draufsicht. Kugel A soll durch einen zentralen Stoß die Kugel B über zwei Banden treffen. Konstruieren und Begründen Sie Ihre Konstruktion.
Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren.
_%E2%80%93_Geometrie-Wiki.png)
Betrag(Strecke AB) ist der kürzeste Weg von A über Bande (rechts) und Bande (oben) zu B. Def (Strecke)-Azalea (Diskussion) 18:22, 6. Dez. 2018 (CET)
1. Mittelpunkt von 
konstruieren.
2. P an der Unterkante spiegeln, B an der Oberkante spiegeln.
3. 
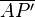konstruieren, mit dem Schnittpunkt S1 
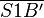konstruieren, abschließend 
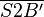.--CIG UA (Diskussion) 11:30, 7. Dez. 2018 (CET)
auch eine schöne Lösung! -Erklärung?--Schnirch (Diskussion) 11:58, 10. Dez. 2018 (CET)
Da A und B den gleichen Abstand zu P haben ist die Verbindung jeweils eines Punktes zu P (die kürzeste über die jeweilige Bande) auch gleichzeitig vom Betrag und von den Winkeln gleich der anderen. Bzw: Wenn wir P als Spiegelpunkt nehmen, dann wird A-S1-P auf P-S2-B abgebildet und andersherum.--CIG UA (Diskussion) 11:14, 14. Dez. 2018 (CET)
