Diskussion:Die Höhen eines Dreiecks: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: =Möglicher Fehler im Skript?!= Meiner Meinung nach kann man einige Dreiecke konstruieren, bei denen sich die Höhen (nach unserer Definition) nicht in einem Punkt sch...) |
(→Aufgabe 14.1) |
||
| (8 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
===Beispiel=== | ===Beispiel=== | ||
<ggb_applet width="957" height="540" version="3.2" ggbBase64="UEsDBBQACAAIAM+l9DwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vrdbts2FL5en4LQgGG7sCJS/6vdInGHrUC2FEvbi90EtETbXGTJlejE7tCHWgvsBXbfZ9ohKcmyHSVx4qx1N11Y1tERefh954ek1H06nyToguUFz9KegU3LQCyNspino54xE8NOYDx98qg7YtmIDXKKhlk+oaJn2CYxpHzGnzz6qluMs0tEE6XymrPLnjGkScEMVExzRuNizJhYkdPZnCec5ouTwe8sEsXyhm7keTqdQS8in4EsmsTHvKguD1SH04SLZ/yCxyxHSRb1DM8F0+Hfa5YLHtGkZziWlpCeQdZugsiWd8dZzt9mqZDqy8aHIEGo4G8ZIEKkrHugBtplsyjhMaepHIyyA5QQuuSxGPeM0PWhScZHY7DVtQPdWpRleXy6KASboPlvLM/AVkvivNAXjueYxAWowC7ZISYmXC1WLlVD7OKUCQHEFIjO2RKyUc7jlYvnxVGWLEXTjKeiT6dilitW7VJ0KhayB7AklyYfpqOElTICoI9ZdD7I5qcaBls3/XIxVY8ogwajfpZkOcolwGDzqDwP9FnpSEtrLUvpWEqjbEM2Wt/HIVEa6jzQZ6WV8FSbVo4cV6PGVtUNL5AUQOPSGevBJ3TAgFwDzVIujqsLcILzcqhYP/DLbDKAKGi6Qd0m3lWb3YM1B+qeszxliXaTFLidZbMCXUh31H0pQ2IW8Qlc6hslJFTS9QoM0NKYjXJWGa5jSAOm7lpNV1wTdw8qI6QNBdgaCUgGMB4hxyJjVUCcyH8xFVIiAyFhEwZRIpQ/KHeqcTk06pSQqeiu4ri8v0QYbl/pG8qLaDIdU5CYpfEJXUCsN4ej2vs5i1cHSVMAS40AQm4qG5B0TBnTTIrSg9EUGlTx0EBaAVSguXyKOBCFMiX64IxvdW5USjp4ZOCrbu2SWY3IDdj0vwRsZO6X0Nim6+0OmqMvARqduyUinmc1D7wdUFE2mdA0RimdQLcvsmQxylIFEJeVEVFLxhmiWOKGKJGepbGZieo+pJgEcjjWagOtRuFk94xId1h2cwUzusMK+7qp1WQsxpDzUlYUqmKIZm1o57GBW5NI7NqKSheX5WHJJN6GyXZ3K9hIXtWGDD7NaLb0y2ZKstyweQS28jViEh2GHdsMLdzU8dfL5zVjZG9SrVPoIsYnMMeKuKj9KpF+/zwVUNKYKhGbleqcsamcIpykL3OaFnKyqHUaFfCW7NA9Y6eDzVDRYZn+SuRbunxAsgz8Jnv7S020Z9RgM9C1vEPMUIeKY3oO/P2MKVitAMdgY1v6X8/78fW5XQ63ZiF+QCpXZ/v7nQC3Yqbfxgzbghm2T8xUua/Tkvw6D5X97hIxmzOl4Ra8DPeJl06d+urM19lp6mvH/ySHVSPMIWnSHiHxBhOjLZgY3ZGJ1VX8v0aFzlKLljQGzPimhYGtT0pMGSJsg5jxFsSM94qYq1LWokxpOnU59icOlyPNSrTBCt+CFb5XrOh8tagmb5IIbJmO6zx8gNSTuDUWIs0C32Dh+IzctJxubnRI9btsdXiOAlmeBvq0A5iJaQehr6G2AfQwCDGpIkEDj4mJHZ/cZeOiDUqmoRxfASXeDkr82UAZmoQQuznFkZg6kNS9oFxz4NVE4+4S0lFbST0+s7eD1P5sIMWeaYWut5w4BgrTwLRDz126qd5bc00MR6Oq3gXd03Kpu4qtjNiWKf34bHA9uuuLZ/nADmaQN++G7mhib7meG8jJe+DbrovdcgrjSVo8jwQWCV3LCapa6dvYd3xsEYJJ4HrB/iyx26gv908Pr6Cebkv9Tja1dkn9yXBYMKGXCppa4t/OM+RSzwHyiReUP/Uei2WFtnQa/SNfiqr9L8+2fT+EuMXyx9qj3Zc217DbFpTjsxs22DddYyebag/kGrqUkVs6BsycsU9s4jvAd2B75S6NXPZYgUzMju0EVgiuUObt0LVDxwpsN8C4em+8D26h3pivOYUksqUQf/zzep9Qb3RrKkFbPg+mzEqkHdPHxA6CMLDswPHCe20yYGvTH277nmXjpfw1FNE8ahTfSpgk2eWvbJiwucJwjZTtEC/xLgvxKuLvt0L8/Tri2HR9C8qcTaDYOQHUu/8xr0tfy0bBxw9bYf7hRsyD/wTmbD7NoWH5/rkc1ks2FzD3gBs945s3s0w8fsaGPOXqHfX36Nuf/v5rzBAD4wr0LGecRecForOhEuXolHHBUNy4+d03X2PrsfpB5fFDgQrG0R+HR/138rlK11zReiUTKJJfWuk+m42Wz8p+47pXkL1TH5UJNhYI3ADFtEDHmUAXYHtfa3OGfmQ5BbDR4dF9O5Si1g7R4UaPR/17D/G6Ho82h9g3kWZRMb8aEwKoNlZ5v4fL33v6Xwiaixdy3YT0Vgy2vMbhO2U9d0lT7LnNTxyavn3Q/K5IfUxXfk345B9QSwcIp/iSUhAHAAB/KAAAUEsBAhQAFAAIAAgAz6X0PKf4klIQBwAAfygAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAABKBwAAAAA=" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | <ggb_applet width="957" height="540" version="3.2" ggbBase64="UEsDBBQACAAIAM+l9DwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vrdbts2FL5en4LQgGG7sCJS/6vdInGHrUC2FEvbi90EtETbXGTJlejE7tCHWgvsBXbfZ9ohKcmyHSVx4qx1N11Y1tERefh954ek1H06nyToguUFz9KegU3LQCyNspino54xE8NOYDx98qg7YtmIDXKKhlk+oaJn2CYxpHzGnzz6qluMs0tEE6XymrPLnjGkScEMVExzRuNizJhYkdPZnCec5ouTwe8sEsXyhm7keTqdQS8in4EsmsTHvKguD1SH04SLZ/yCxyxHSRb1DM8F0+Hfa5YLHtGkZziWlpCeQdZugsiWd8dZzt9mqZDqy8aHIEGo4G8ZIEKkrHugBtplsyjhMaepHIyyA5QQuuSxGPeM0PWhScZHY7DVtQPdWpRleXy6KASboPlvLM/AVkvivNAXjueYxAWowC7ZISYmXC1WLlVD7OKUCQHEFIjO2RKyUc7jlYvnxVGWLEXTjKeiT6dilitW7VJ0KhayB7AklyYfpqOElTICoI9ZdD7I5qcaBls3/XIxVY8ogwajfpZkOcolwGDzqDwP9FnpSEtrLUvpWEqjbEM2Wt/HIVEa6jzQZ6WV8FSbVo4cV6PGVtUNL5AUQOPSGevBJ3TAgFwDzVIujqsLcILzcqhYP/DLbDKAKGi6Qd0m3lWb3YM1B+qeszxliXaTFLidZbMCXUh31H0pQ2IW8Qlc6hslJFTS9QoM0NKYjXJWGa5jSAOm7lpNV1wTdw8qI6QNBdgaCUgGMB4hxyJjVUCcyH8xFVIiAyFhEwZRIpQ/KHeqcTk06pSQqeiu4ri8v0QYbl/pG8qLaDIdU5CYpfEJXUCsN4ej2vs5i1cHSVMAS40AQm4qG5B0TBnTTIrSg9EUGlTx0EBaAVSguXyKOBCFMiX64IxvdW5USjp4ZOCrbu2SWY3IDdj0vwRsZO6X0Nim6+0OmqMvARqduyUinmc1D7wdUFE2mdA0RimdQLcvsmQxylIFEJeVEVFLxhmiWOKGKJGepbGZieo+pJgEcjjWagOtRuFk94xId1h2cwUzusMK+7qp1WQsxpDzUlYUqmKIZm1o57GBW5NI7NqKSheX5WHJJN6GyXZ3K9hIXtWGDD7NaLb0y2ZKstyweQS28jViEh2GHdsMLdzU8dfL5zVjZG9SrVPoIsYnMMeKuKj9KpF+/zwVUNKYKhGbleqcsamcIpykL3OaFnKyqHUaFfCW7NA9Y6eDzVDRYZn+SuRbunxAsgz8Jnv7S020Z9RgM9C1vEPMUIeKY3oO/P2MKVitAMdgY1v6X8/78fW5XQ63ZiF+QCpXZ/v7nQC3Yqbfxgzbghm2T8xUua/Tkvw6D5X97hIxmzOl4Ra8DPeJl06d+urM19lp6mvH/ySHVSPMIWnSHiHxBhOjLZgY3ZGJ1VX8v0aFzlKLljQGzPimhYGtT0pMGSJsg5jxFsSM94qYq1LWokxpOnU59icOlyPNSrTBCt+CFb5XrOh8tagmb5IIbJmO6zx8gNSTuDUWIs0C32Dh+IzctJxubnRI9btsdXiOAlmeBvq0A5iJaQehr6G2AfQwCDGpIkEDj4mJHZ/cZeOiDUqmoRxfASXeDkr82UAZmoQQuznFkZg6kNS9oFxz4NVE4+4S0lFbST0+s7eD1P5sIMWeaYWut5w4BgrTwLRDz126qd5bc00MR6Oq3gXd03Kpu4qtjNiWKf34bHA9uuuLZ/nADmaQN++G7mhib7meG8jJe+DbrovdcgrjSVo8jwQWCV3LCapa6dvYd3xsEYJJ4HrB/iyx26gv908Pr6Cebkv9Tja1dkn9yXBYMKGXCppa4t/OM+RSzwHyiReUP/Uei2WFtnQa/SNfiqr9L8+2fT+EuMXyx9qj3Zc217DbFpTjsxs22DddYyebag/kGrqUkVs6BsycsU9s4jvAd2B75S6NXPZYgUzMju0EVgiuUObt0LVDxwpsN8C4em+8D26h3pivOYUksqUQf/zzep9Qb3RrKkFbPg+mzEqkHdPHxA6CMLDswPHCe20yYGvTH277nmXjpfw1FNE8ahTfSpgk2eWvbJiwucJwjZTtEC/xLgvxKuLvt0L8/Tri2HR9C8qcTaDYOQHUu/8xr0tfy0bBxw9bYf7hRsyD/wTmbD7NoWH5/rkc1ks2FzD3gBs945s3s0w8fsaGPOXqHfX36Nuf/v5rzBAD4wr0LGecRecForOhEuXolHHBUNy4+d03X2PrsfpB5fFDgQrG0R+HR/138rlK11zReiUTKJJfWuk+m42Wz8p+47pXkL1TH5UJNhYI3ADFtEDHmUAXYHtfa3OGfmQ5BbDR4dF9O5Si1g7R4UaPR/17D/G6Ho82h9g3kWZRMb8aEwKoNlZ5v4fL33v6Xwiaixdy3YT0Vgy2vMbhO2U9d0lT7LnNTxyavn3Q/K5IfUxXfk345B9QSwcIp/iSUhAHAAB/KAAAUEsBAhQAFAAIAAgAz6X0PKf4klIQBwAAfygAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAABKBwAAAAA=" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| − | Bei diesem Beispiel gibt es keinen Höhenschnittpunkt, den Höhenschnittpunktsatz demnach auch nicht. | + | |
| + | <br />Bei diesem Beispiel gibt es keinen Höhenschnittpunkt, den Höhenschnittpunktsatz demnach auch nicht. | ||
Das Problem hierbei könnte sein, dass wir die Höhe h_c dem Lot von Punkt C auf AB gleichsetzen (nach Definition). Wäre mit Höhe eine Gerade (Lotgerade) gemeint, würde der Satz stimmen...oder liege ich da falsch??--[[Benutzer:"chris"07|"chris"07]] 19:07, 20. Jul. 2010 (UTC) | Das Problem hierbei könnte sein, dass wir die Höhe h_c dem Lot von Punkt C auf AB gleichsetzen (nach Definition). Wäre mit Höhe eine Gerade (Lotgerade) gemeint, würde der Satz stimmen...oder liege ich da falsch??--[[Benutzer:"chris"07|"chris"07]] 19:07, 20. Jul. 2010 (UTC) | ||
| + | <br /> | ||
| + | <br />Wie ist es, wenn die Höhen verlängert werden, wir also für die Länge der Höhe zwar die Länge der Lotstrecke verwenden, als Höhengerade jedoch "das Lot" / die Lotgerade benutzen, schneiden sich dann nicht die Höhen außerhalb des Dreiecks? --[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 22:53, 20. Jul. 2010 (UTC) | ||
| + | |||
| + | <br /> | ||
| + | <br />Dem stimme ich völlig zu, nur dann wäre der Schnittpunkt ein Punkt den alle drei HÖHENGERADEN gemeinsam haben und nicht die Höhen selbst, oder? Denn laut Definition ist ja die Höhe gleich dem Lot. So haben wir das doch extra definiert.--[[Benutzer:"chris"07|"chris"07]] 08:11, 21. Jul. 2010 (UTC) | ||
| + | |||
| + | <br /> | ||
| + | <br /> Stimmt, genau genommen müsste man von den Höhengeraden sprechen. Allerdings müsste man dann doch noch definieren, was unter einer "Höhengeraden" verstanden wird... also dass sie der Lotgeraden entspricht... oder?--[[Benutzer:Löwenzahn|Löwenzahn]] 09:03, 21. Jul. 2010 (UTC) | ||
| + | <br /> | ||
| + | <br />Ja, stimmt genau!--[[Benutzer:"chris"07|"chris"07]] 09:06, 21. Jul. 2010 (UTC) | ||
| + | |||
| + | |||
| + | <br /><br />Kommentar --[[Benutzer:*m.g.*|*m.g.*]] 19:46, 21. Jul. 2010 (UTC): | ||
| + | |||
| + | == Aufgabe 14.1 == | ||
| + | Es sei <math>\overline{ABC}</math> ein Dreieck. <math>\ l_c</math> sei die Lotgerade des Lotes von <math>\ C</math> auf <math>\ AB</math>. <math>\ l_a</math> sei die Lotgerade des Lotes von <math>\ A</math> auf <math>\ BC</math> und <math>\ l_b</math> sei die Lotgerade des Lotes von <math>\ B</math> auf <math>\ AC</math>. Man beweise: <math>\ l_c, l_a </math> und <math>\ l_b</math> haben genau einen Punkt gemeinsam. | ||
| + | |||
| + | [[Lösung von Aufgabe 14.1]] | ||
| + | |||
| + | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 16. November 2010, 22:18 Uhr
Möglicher Fehler im Skript?!
Meiner Meinung nach kann man einige Dreiecke konstruieren, bei denen sich die Höhen (nach unserer Definition) nicht in einem Punkt schneiden.
Beispiel
Bei diesem Beispiel gibt es keinen Höhenschnittpunkt, den Höhenschnittpunktsatz demnach auch nicht.
Das Problem hierbei könnte sein, dass wir die Höhe h_c dem Lot von Punkt C auf AB gleichsetzen (nach Definition). Wäre mit Höhe eine Gerade (Lotgerade) gemeint, würde der Satz stimmen...oder liege ich da falsch??--"chris"07 19:07, 20. Jul. 2010 (UTC)
Wie ist es, wenn die Höhen verlängert werden, wir also für die Länge der Höhe zwar die Länge der Lotstrecke verwenden, als Höhengerade jedoch "das Lot" / die Lotgerade benutzen, schneiden sich dann nicht die Höhen außerhalb des Dreiecks? --Heinzvaneugen 22:53, 20. Jul. 2010 (UTC)
Dem stimme ich völlig zu, nur dann wäre der Schnittpunkt ein Punkt den alle drei HÖHENGERADEN gemeinsam haben und nicht die Höhen selbst, oder? Denn laut Definition ist ja die Höhe gleich dem Lot. So haben wir das doch extra definiert.--"chris"07 08:11, 21. Jul. 2010 (UTC)
Stimmt, genau genommen müsste man von den Höhengeraden sprechen. Allerdings müsste man dann doch noch definieren, was unter einer "Höhengeraden" verstanden wird... also dass sie der Lotgeraden entspricht... oder?--Löwenzahn 09:03, 21. Jul. 2010 (UTC)
Ja, stimmt genau!--"chris"07 09:06, 21. Jul. 2010 (UTC)
Kommentar --*m.g.* 19:46, 21. Jul. 2010 (UTC):
Aufgabe 14.1
Es sei  ein Dreieck.
ein Dreieck. 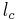 sei die Lotgerade des Lotes von
sei die Lotgerade des Lotes von  auf
auf  .
. 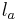 sei die Lotgerade des Lotes von
sei die Lotgerade des Lotes von  auf
auf 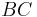 und
und 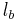 sei die Lotgerade des Lotes von
sei die Lotgerade des Lotes von  auf
auf 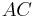 . Man beweise:
. Man beweise: 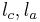 und
und 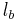 haben genau einen Punkt gemeinsam.
haben genau einen Punkt gemeinsam.

