Erarbeiten von Sätzen: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Den Satz über die gegenüberliegenden Winkel im Sehnenviereck entdecken) |
||
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
=Das Whiteboard der Sitzungen vom 25. Mai und vom 8. Juni zur Satzfindung= | =Das Whiteboard der Sitzungen vom 25. Mai und vom 8. Juni zur Satzfindung= | ||
[[Datei:WB erarbeiten von Sätzen.svg|Leitideen II, Didaktik der Geometrie, Erarbeiten von SätzenWitheboard zu den Veranstaltungen am 8.6. und 25.5. 2020]] | [[Datei:WB erarbeiten von Sätzen.svg|Leitideen II, Didaktik der Geometrie, Erarbeiten von SätzenWitheboard zu den Veranstaltungen am 8.6. und 25.5. 2020]] | ||
| + | =Den Satz über die gegenüberliegenden Winkel im Sehnenviereck entdecken= | ||
| + | == Video== | ||
| + | <iframe width="560" height="315" src="https://www.youtube.com/embed/Gslbz6kTz0A" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe> | ||
| + | |||
| + | == Das Wesentliche des Videos == | ||
| + | === sehr speziell: Quadrate === | ||
| + | Jedes Quadrat hat einen Umkreis und ist somit ein Sehnenviereck.<br /> | ||
| + | [[Bild:Quadrat_als_Sehnenviereck.png]] | ||
| + | |||
| + | === weniger speziell, aber immer noch ziemlich speziell: Rechtecke === | ||
| + | Jedes Rechteck ist ein Sehnenviereck. | ||
| + | <ggb_applet width="419" height="444" version="3.2" ggbBase64="UEsDBBQACAAIAEKv9TwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VrLcts2FF03X8HhXjQeJEjMSMlIdheZSetMnWbRTYYiIQk1RaokZEv+qyb5jn5TLwBST0s2/Yhjz3ggXoDAxTn3XDyk7rvFNHOuRFnJIu+52EOuI/KkSGU+7rlzNepE7ru3b7pjUYzFsIydUVFOY9VzqUdcbZ/Lt29+6VaT4tqJM9PksxTXPXcUZ5VwnWpWijitJkKoLXs8X8hMxuXyfPi3SFS1rrCdvM9ncxhFlXOwJdP0g6yaxxMz4CyT6kxeyVSUTlYkPZcF4Dp8+ixKJZM467k+shbSc8lOJZiorp0UpbwpcqWbrzsfgcVxKnkj4E2kbd0TM9GumCeZTGWc68kYP6CR41zLVE1gQMyhSyHHE6VH57a3pCjK9GJZKTF1Fn+Jsui5Hcy8wA8JxZwGiIUsCF1naes493yMQ59w5gc0wBhABI/BFco9gpgfhhjmSjAK4J2DVWZocXUhlAIqKydeiDXI41KmWw/vq0GRrU2zQubqNJ6peWnigNamC7XUowFwpZ5kPx9norYRoGkiksthsbgwwGFqu/60nJlXjEPD8WmRFaVTakrA/3FdDm1p2mhPV62QaYNMi7oP3emqHnNiWphyaEvTKpO5da2eOW5mjVEzjKwcbYDOdfiuJp/FQwHh4DrzXKoPzQOEzWU9VWxf+H0+HYJuNgNn1Sd+qj67Jzsh170UZS4yG1g5cDsv5pVzpQPYjmUcSUUip/BoK2pIYk3Xn+CAtaZiXIrGcas6C5ipRZvBu2PunjROaB8q8DVRkD5gPkrPRatbgbJ67tQbe66TxkpbtXwyMRWgLWViwoTUCpvf3FUiKUxOaNRf169Rhupb48NEUpzNJjFYvHoCWbyEDLE5JdPf+WhUCeUsQIug2SWEON2o/a1It2GIc4DTzBFkPNPda8JmQqR1zlR1lDszGNBoZoMNA2KlB2O6LYzWofrDjX3ZtLH60tnEjEtr8i1gd0A3+IL3wduOvA1vngK+ZwOI1wChtvgkxXQa56mTx1MY51SWSSYMKFKvJE6MdIQ5MbZoWSDmqqlKbHd1J3twQ5TLZIVl4m4nGDUBHeeiqkwWVJv57nA434MQ9HA67uUcLFQivwLXirJynAWqmVqiBv7GsgDUOsa0xLXpBm9wA8yXcuH0m/b9plVfL73M41t/DOy0HqLvQ89GFP1A7ykaz/7JrfeVzY4QSIkcyeQ46R+NKLY5T/ao7h+neltZ/QclJUzs0mbKhycm4hspkOhHCI94lDKKCUJRGFEW4sAmqsDDlPtgCaA+IBF7jCw/QFjuENS3olz0Yenc4yo+zpWO8hUV8QNV2TpPPkKWa7hRnedwnef2YW6h4x21yClsjhOpjnPxPlew0wAI9hRjCImh0OptprjByqCNggYPUhDzDeC6GNqitXyIBZji+xHCPcYoi0LOMcGMguiePvzPS9gWjYs8zm4RwqDBfRfuYQsRDF+VCDp4Z7XfJ+G5VXCUkv4hStIWlKSvm5Jb1oUXzkzDw5nptE1mOv2xmal97kFexFAABh+q/RD7+DHJ5w5U08OonrVB9eyl8n2HUAsbDu+H+qEdzy7sAXkM7B+LbAn55fbMMrCgn0JBa5y3kIcjfyaSS1znoS/Yth+aD/BGYj7AHjq1Z5pjJFk3GhpWPT/fUQYH1JAa4L30hNso5fApuBJj/bTeAn55ofk8ehsYepSENAx4RHxKWGC3GTT0WBBxwlFEw9BH/hOlXhNjmT4MrJICHCD2b5EuhZjp67vz/FMZ55W++rVtNm6n7knN8NVR0/E9EkachRTp/yDEW+uijz19dYt8HrIo4E+1Kr4ANcmrowZ7GCNCKCI+IwEOWPBrp8netyupwzygEJ4jjCKCOX69dKWvjq5dIaFgS0kd7nEeIkRCRDkKafBUZ99nIWd7dTffgOys7Wd2te7btXqwt6j/9+/xpdpc0694gtb6ffBnXuPreyEmNIp4hGjkM34X08cuzjHaPzscX5w3NlzY3pwf2G+1kVhcJusNVdQYs6y4/kOMMrEwMO/w1o6U3Q3XHilfW5Hy9aclpT48YP4KSKmVcnpQKd9akfJtlxTsQbIJOZyoWMh9SEHs5Wjh9eHk9q+Zfi5earGcHRTL91a8fL+Tl+jlchirebn9mvBH8nKy+V2q+clB/ZuLt/8DUEsHCFxRBbNRBgAApSEAAFBLAQIUABQACAAIAEKv9TxcUQWzUQYAAKUhAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAiwYAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| + | === noch allgemeiner, aber immer noch ziemlich speziell: gleichschenklige Trapeze === | ||
| + | Jedes gleichschenklige Trapez ist ein Sehnenviereck. | ||
| + | |||
| + | <ggb_applet width="419" height="411" version="3.2" ggbBase64="UEsDBBQACAAIAJGx9TwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VrbbtvGFn1uv4LgQ9GiNT1XcohaKWT7JUDcFHVOcNALCoocSVNTpEqOHMkH56OK/sf5prNnhpQlSpYtxU7sPITi3Getvfbs2ebJD/NJ7l3LqlZl0fNxgHxPFmmZqWLU82d6eCT8H159eTKS5UgOqsQbltUk0T2fBsQ35TP16ssvTupx+cFLctvkvZIfev4wyWvpe/W0kklWj6XUa+XJbK5ylVSLt4M/Zarr2wo3yOtiOoNZdDWDsnSSvVF1+3psJ5zmSp+ra5XJysvLtOeHHJYOv97LSqs0yXs+Q66E9HzSqYQiamrHZaVuykKb5reDD6HE82p1I6EnMmUnx3ajJ3KW5ipTSWE2Y9cBjTzvg8r0GCbEMQwp1WiszeyxGy0tyyq7XNRaTrz5L7Iqe/4RDgPOIkJxTDkKo5BHvrdwdXEcMIwjRuKQccoxBhBhxbAUGgcEhSyKMOyVYMShz51Vdmp5fSm1BiprL5nLW5BHlcrWXl7Xp2V+WzQtVaHPkqmeVdYOaFN0qRdmNgCuMpvsF6NcNmUEaBrL9GpQzi8tcJi6od8tpraLXdBgdFbmZeVVhhJY/6h5DtzTtjErXbZCtg2yLZoxzKDLehwT28I+B+5pW+WqcEtrdo7bXWPUTqNqzxTA4MZ8l5vPk4EEc/C9WaH0m/YFzOaq2Sp2HX6cTQagm1XDWY6JH2vMk+OOyZ1cyaqQuTOsAridlbPauzYG7OayC8lkqibw6ipwszpD179gAa40k6NKtgt3qnOA2Vq0aryd4pPjdhFmDTWsNdXgPmA/2uzFqFuDsnr+JBgFvpcl2pQa+eRyIkFb2tqENaklNhf+0pGU1ie06m/qb1GG6q32YS0pyafjBEqCZgN5sgAPsbolO97b4bCW2puDFkGzCzBxulJ7UWbrMCQFwGn3CDKemuENYVMps8Zn6sbKvSlMaDWzwoYFsTaThaYtzHZEzY8b19m2cfoy3sTOSxvyHWD3QHf6B94Eb93yVlbzGPA9GUBxAxDaF5+0nEySIvOKZALznKkqzaUFRZmTxEuQsTAvwQ4tB8RMt1WpG64ZZANusHKVLrFM/XUHo8eg40LWtfWCetXf3W3ODyAEHU7HgxYHB5UsrmFpZVV73hw1TC1QC39bMgfUjmzRAjdFN3iFG2C+UnOv37bvt6365ugNg3jtXwjltJmiz2BkK4o+NzFFu7K/Crf62nlHMKRUDVW6m/SfrCjWOU83qO7vpnpdWf2DnBIm7mizz8MdEyNWCoR9CuHRAPOY4AhHIsaYsZA3OsQQgggSCYEQJSI0Wzlcl2/ALjsM9Z0q5304OzfISnaTZcx8yUVyoCz3dpQfoctbvFHj6HDj6I62Ib2HljuKURMIkFOld9PxutAQbQAKG6qxnCTwMApud7lCzOk+Kjo9SEUhs5ibx8A99pYQcRhT/DBORCAYigQREEELwTl9Cgm8rSA2GpVFkm8Rw2kLfBfvwR5CGLwoIRzhzpG/ycJTy2AnJf27KMn2oCR72ZRsORyempMtTFzsOinkHmzIF8VG96RYRklPiP6lHJny7VI43QB/uBv8uhltidzzD6A34edBKDAPechACBFGYXtsCy5izmLKEBIIi0fixuKbm4BteUhDkLd507+ScmpSLG+Ld1VS1CY959qsZBAOcXuN2IYbXI/2ENroRQntaAvFq06QBUjENKaCUxSSkD25Cu8Kz0Z3cXPmrrYPjcvODs4bHByb7YAfx9Tgj4kQcPojhl34xQKIuwhEAgwTKhiPHRkkIEZtArOQhhHlh4Ri56rWSZHeYfpnW/IEycD0yC7OdsNczCayWskY3HYz48HSZu0Cu7Fl+HA7xxspovm0Auszd8Fm3ndyrmFSD2p6/ld/zUr9/W/ltayMzf7HvXvfel//CGj8evH7N8vfsHX75pr81/vtO69n/lt2ud2Qd7yxew2z+p0lfFaJq/pN8k7+e90vwnp0UmmbNHAAXajM2s+vF995BoHdKbgux+Mutyhg97q2+5OaG4w/YNvLfO/hqYFdoskT3ZWM0YoVzdHX42/crfFi0zt9lUzL+vu9PFTT5fl6KeTyJEeYRgE3hTTixlER/nh+asvx3AJzx0Gg9jik1aMc0vtZ8scHw4IGDI4FuChC8IWpyZUB3JHAAY1iSmgMJDDRKuazpVCUEwPekkI530cI5582hbJLAEHMREw4pjFjEPGyyAmABSSEF4oxJwhTzD4mSfIwVLclpu45mTvu5fmgCn05RhETIeI8xvFToPpTmS8g3u9get6EOw5Tk4GiTZZ8Ddj3CoZNrxo/n1mHD+1T+wN6DOwPBsHO/UGoW0aL8nLkp7sVYpPLA844PvhQRbvDge4dN/vjM+3no12rCDAimMURwRCa0pi0tx+ORRzDrYjgEAz1Od9zd1OTvjhqwA0wjENwDHBJQCxEy6gjIEBWTBA44wiFjDVRRxxgwVkYQVtGEYvDl8vW4MWx1QppWz7hxlS/oIzRbm6SF8fNQ4UErNj0HqZBxCHOgaCSIMIivPF50XNia/24t59nbT/s++1h3z3l//f37rPbfkO0JA5ady69OBAUPI9gMeZg3pyL+8jfdXHAaN9L8Mqfz4lwN4Xtfz7f52aQVOltjCXawjwvP/wsh7mcW6A7zB1Ey9mdtPyzFy3/dGlhQQyeBkyfweU0BnY+Gyu8Edz2z60+JSvHq9+u2U88m29cX/0fUEsHCCkjpU3sBwAAFSsAAFBLAQIUABQACAAIAJGx9TwpI6VN7AcAABUrAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAJggAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| + | === allgemeines Sehnenviereck === | ||
| + | Ausgangslage: <math>\ \overline{ABCD}</math> ist ein gleichschenkliges Trapez. | ||
| + | |||
| + | Arbeitsauftrag: Bewegen Sie den Punkt <math>\ C</math> auf dem Kreis. Beobachten Sie, wie sich der rote und der blaue Winkel verändern. Was vermuten Sie bezüglich der Größe von <math>\ \gamma</math>? Was vermuten Sie hinsichtlich der Größen der gegenüberliegenden Winkel im Sehnenviereck? | ||
| + | |||
| + | |||
| + | <ggb_applet width="419" height="411" version="3.2" ggbBase64="UEsDBBQACAAIAJKz9TwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vpbb+M2Fn7e/gpBD0WLrRXeSaHxFE7yMsCkU2xmB4ttF4Us0bY2suRKcsaeRX9UL79jf9MekpLje2LnMhNg52FkkxR5+H3nOzw88el3s3Hm3eiySou86+MA+Z7O4yJJ82HXn9aDjvK/e/XF6VAXQ90vI29QlOOo7vo0IL5pn6avvvjLaTUqPnhRZoe8T/WHrj+Iskr7XjUpdZRUI63rlfZoOkuzNCrnb/v/1nFd3Xa4SV7nkymsUpdTaIvHyZu0ar+e2AUnWVpfpDdpoksvK+KuLziYDp/e67JO4yjr+gy5FtL1yVonNFHTOyrK9GOR12b47eQDaPG8Kv2o4U1k2k5P7EZP9TTO0iSNcrMZawcM8rwPaVKPYEEcwpQ6HY5qs3roZouLokyu5lWtx97sn7osun4Hi4AzSSgOKUdCCi59b+76wjBgGEtGQsE45RgDiGAxmELDgCDBpMSwV4IRh3d2dtml9c2VrmugsvKimb4FeVimycqX19VZkd02TYo0r8+jST0trR/QpumqnpvVALjSbLKXDzPdtBGgaaTj634xu7LAYeqmfjef2FesQf3heZEVpVcaSsD+YfPsu6cdYyxdjEJ2DLIjmjnMpIt+HBI7wj777mlHZWnuTGt2jttdY9Quk1aeaYDJjfsuNp9FfQ3u4HvTPK3ftF/Aba6brWL3wvfTcR90s+w4iznxY815erLmcqfXusx15hwrB26nxbTybowDu7WsIYmO0zF8dR24sc7Q9XcwwLUmeljq1nCnOgeY7UXLzrvWfHrSGmFsqMDWuIbwAfupzV6MumtQVtcfB8PA95KoNq1GPpkea9BWbX3CutQCm0t/EUgKGxNa9Tf9tyhD91b/sJ4UZZNRBC1Bs4EsmkOEWN6Sne/tYFDp2puBFkGzc3BxutR7WSSrMEQ5wGn3CDKemOkNYROtkyZm1o2XexNY0GpmiQ0LYmUWE2YsrNah5sNH97Id4/RlooldlzbkO8DugO7sZ7wJ3qrnLVnzGPA9GUBhAxA6FJ+4GI+jPPHyaAzrnKdlnGkLSmpOEi9CxsO8CDu0HBDTuu2K3XTNJBtwg5en8QLL2F8NMPUIdJzrqrJRsF6Od7vd+R6EoOPpuJdxcFDp/AZMK8rK82aoYWqOWvjblhmg1rFNc9w0fcRL3ADzZTrzeu34XjuqZ45eEYQr/wS002aJHoOZrSh63OQUrWW/5M76ykVHcKQ4HaTxftJ/sKJY5TzeoLq3n+pVZfWOCkqYuKPNPo8PTIxYKRD2HMKjAeMhxlQxzgkmglMXqERAQykoxkIyRiRlD5HlG3DLNYJ6TpSzHhydG1xF+7kyXr6gIjpSlQfHyQfI8hZu1MQ53MS5TZgP0PGaWtIxJMdxWu/n4nVeQ6YBEGwoxhISwcOot93iEitnhyjo7CgFCWYBN4++exwsH+IApvh+hChIyJFSAnPGpLJ+/uju/7aEtGhY5FG2RQhnLe7rcPcPEEH/RYmgg9dO+00SnloFeynp7aIkOYCS5GVTsuVceGpOtjBxue+U0AewoV8UG+unxCJBekL0r/TQtG+XwtkG+IP94FfNbAvkPv/ceRN+HiCFpSQUqZBLJhR3bJCAgzIQC1EoKJWPpQyLb2ZytcUZDfnd5iX/WuuJqa68zd+VUV6Zypwbs1Q8OCbsNWIbbHA9PEBowxcltM42ipejIAqAZSBZcQqJgMJPLsNd6dlwFznn7lp737zs/OiawdG52R784cAPQiYYVwohOGfa2wcWPIBvRmJYKhYKZekgPFCEMRTCaKREW/M7LBu7SKs6yuMd3n++pUoQ9c0byeX5fqDz6ViXS/WC29fMfGDatDVwLbnk9/d0vFEfmk1KcD9zEWyWfadnNazpQU/X//KXaVF/+1Nxo0vjtP9x372/el99D2D8ePmvrxefYef2mxvyq/fTN17X/Ld45XY/3snG5mtY1V8z4ZOKPK3eRO/0P1YjI9hTR2VtKwYOoMs0se7z4+U3nkFgf/1tneLROrUQL+4MbndXNDcYv8e2F8Xe4+sC+zSTRfW6YoxUrGY6X42+dtfGy83w9GU0KapvDwpRzSufb5hi0oUpRgIqBUeYc0oIx/LxotSW87nFZcdBkB5wSqePckof5sgPz4YpDgjkWxIJLAFt3sCNeUCZlBR4oUIS9alLKKnTAt5SQrk4RAcXz1tC2ef/AfhySCg4NQ0RVYCxO6YDAW7OJKcUERIic3wfXyaxf1Zcg/TCQdpzkG5eQ/77235E7d++FojB6LV4zcwfXSH3g50xGkKed9cdZJ/PY3Ro+F6q+mJXecJ7q773cuqojG8xl21jlhUf/qYHmZ5ZnNduFQ+trt+RGq0F+Gevrh9WPr938RzDuphIRUMMDgTngFjoghAmFVeESMZBMA/RxQ9FNoc7266buVUG5GQRbeLLCjHvU5g2vm5O6sge2TC+bz/AG7H9wLp+cvc9wpnRsrSY+elu9vY+AOBzfHRahPYndOt1iujnT7Sf/xcr7uSm/+K46bBASkhUCFccC4VD0ZT1mMQqhK4wJIIogi1VHAUEIRFSrhiVYYjEy+UqfnFcmVCuQDYhR5IpSCSRdLWgjgoQxUogJhnCTDR/C+pgGhAsGJMESQUp0KNVyD8BXcmLowuUxYUAniApxWGbkRplgcwQHMYQ85QiLgh2zG8RRBjCFQGa+WeurHtnxec7s+I/DsqK/1jPiuGeJUIWCqmEYiFnrWs/V1r8OeS923Bvcq6LNufawP3Pg3D/cwvuEstQELiLIIThHH8I7tt+3sWfGnf1hLif7cT994Nw/33bLRDufgrOZKbCUB15C2x/2trEOfN4PuCPcPiT5V9x2h87N7/2fvU/UEsHCEhVilJbCAAAHy4AAFBLAQIUABQACAAIAJKz9TxIVYpSWwgAAB8uAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAlQgAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| + | == Der Satz über die gegenüberliegenden Winkel im Sehnenviereck == | ||
| + | <ggb_applet width="784" height="1092" version="3.2" ggbBase64="UEsDBBQACAAIANuA9jwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7V3bctvGGb5ungLDZnKTEYw9AkikZCTZVmxJdSd23U7HMx2QXFGwIIAGQFtU24tOzu/RB2jOJyeZae7dV+q/WJDCkSR4kCk5mrFIgiscvu8/77/rzXfPTj3tqQgjN/C3Wkg3WprwO0HX9XtbrUF8tGG13n3ntc2eCHqiHTraURCeOvFWi+i4JY8P3Hde+91mdBw80xwvGfLQFc+2WkeOF4mWFvVD4XSjYyHi3HFncOZ6rhMO77Ufi04cXXyhTnLH7w/gKnE4gGOd0+6BG40+3kgu2Pfc+Kb71O2KUPOCzlaLM7h1ePdQhLHbcbytFjXUEbzVwoUv4RCR3x4HoXse+LEcfnHyIziiaZF7LgARSx7bvJE86KYYdDy36zq+fJjkPmCQpj1zu/HxVsu0KJxSuL1juFdk2IY6XScIwu79YRSLU+3sryIM5Fm5DmOH6hNBXOIewY0JedvywzD7KTmNeHpfxDHwEmnOmbhArBe63RFS8v2daCfwuuOv+4Hrx7tOPx6ECackPXQ/Hsrzw6VCecPbfs8T6TEMkB+Lzkk7OLuvQCDq1A+G/eRPkvtp93YDLwi1UMLLYED62lavyRh5o+NRRjLGSEak55AnHX+PbJyMSF7b6jUZ5bm+urX0wdHooZExuowbafKARBFEcfzwntMWQG1LG/hufDD6ACJwkj4qUn/wh8FpG3QgKwTjc6JlnXPzRkF8Nk9E6AtPyYgP1A6CQaQ9lcKorpXcSFd03FP4qL5IIXEkXX+CG1BHu6IXitGNKw1SgCXf5uSwcHjzxugm5D1EcK+dGEwBPE8sn0VqagxaIt91nVgeSUaenjp+V/OdUzhyx4/hOUGLW/IqrtRczTG2WmfbACGcAG21hsnb5C6CQTwacKhuID2bVC9PnArQvTiRs0RMx3gftsaGJkhsRpGQC+rgQbpu8hRy+L10tJdev/14LHGcJgInX9rqxfH6xw5AM1I6zxmCgcmimFzt3tFRJGLtbKu1AWwPQatw5tvDoFuBfCSHK92GP0venCuLm4xRSinNSfKXJJUYhUgJ8z8m2FThXQR552+oCcxy+BSgM7KZBRNhZQSS19QIzIpnCTHHB5lXFMaiL08gtaovRDd1UnFqirQ+nDIxbJnbusCbpngvCPeuG3Y8UcD7UMl2CnAO9JPJkIOAup0xnietvJGLj8GW+CKKEkscZ23uAuLvlhnLG+Tmsk+4kmXKJ1E504OB0xT+U7jRIIw07cxIWR4aI+pGR87QSHmGKD10jjK8gtSE7pm2PRq/PRq1jaWyJo52m6Rn3aajk22zzIOLJ7664UgZdJC7jnsEjDVWyZOSZGw3UcbtsioqP1/ifFmKmDVsdsKuCoBWracbWOeGgWwDmchG1DZNqmSL6AaxmUkRs7FtmcxmyzabZY52GhnMl8iRsm34Uiwp0U2IaLlJiI1s2+am4gfpQBY3KIPgFyGLGHz1/Ow24Wf30vlZGQVYxzaxqE1AOxghiBAVe+jY5Db8s7BhcsTx6hm42YSBmy/TimGU+qhLsmLAC0OmaTAMpoywlCDDZoQzacbAvhnWYgR5w17gFyjaTmMReMFS5jWHpCzleIO8w4PEDqnRjhrdUaO78AL+UEyjVl1+RN74jPPFMDlBqAssGUkkgaFSpIKaKGIW0/xDRaInP41vxHk5T9PQrGTkDumMIpvbzDIsC2yBct1cJ4aNmckQ/FCbpq6T6YhbBoynjBHMaCnLnhSnFUIj97TvuR03HkuaJ9VjnBGCSpUT2hMh+rKScM9/EDp+JCtKakwmUZ6RqM5VI4rqie3GGFymZdo2GXtRxDAybY5MyjkjfEQVs2yOKdh2YhqI8atLVfeKUQXGxQLAMTJMm9kGI2nAQ3ULm4SbhoXBogOLI6aogSnj3ObgopnFri5T4ooxxXVEICiyITQFLbK4Na6wcM5NDPpkIoIpJnRElQnDGTVsgrhBGFlnqvLO/35KVWUhYrvk7tuTfXmR+PZSChG5yGjGQtx8lYgJMlGVNg5r0szztAhwPaRgpyQFR82k4Oj6SEFVcjqsTGXPs9e56iKwWxKBXjMR6F0fEdioyI6H1an0tZKBcu533EwGjq+VDJQS8GF1tr7+MiDO+iHcicQxxfiBOIshnIIvtlpvPBkE8ds3AaD7Tnyu/fq8DW+7rtB6oif85KPnyrdd4Wt/dv0T4WnuqXZfHPvCf+qKEHJ5dY7kunkRieFCrfxV5woCl0RwFDthnNSrtDS3IpBRZX4Slk0dG9kflC2+TAcW54CVoL6lvfF7ZLx9x9cei64oYKdFLuhnHeB3fBj5TKEeDfp9de1f/x3qs2OO1wxzmpYamNUMWJID9mEQOoMoEvH5wO+9NTsa5KWikTSKRCJ0jy4aXpKGiQ0Qm2jUYFEFHNMNWpZVkGDeDEWaQ/F17VHwVAqcL/6+vbN785/a65obxZpw/XlVnM4O8IrnHUvou9GB80D8JW8q86SoWy1xgis5sXTbZhlLQVJObCtrP3AtQTkg20HgCeeiTuomOMKtDkTJ/l+S+GYnbtXMEcITZm6nCx/LCd+OOHYG/biZ/rIrq7+IZhXYShMLQNbIi1C1sOQjuaT5qhDH7YyS+qRGXw7nXnw+OZ5LOoTGOMLogvwhnWADQ3LMTJNYEAZZU4O5aS0Gj+uIQkaZKtaMqpmCMSfsXMyjWKODnhc8e18ceeIswXnW8LqKlOI0S4mULxqR8kWRFKpDugppCbUtYhKM6eVy0mg6ZfmcjJV9Lk3ZrdWULxuR8mWZFMqRhTFDiGALUfZKKcqcpGyP0tA6TfmqESlflc0XRzZm3KLUtAgl6DdNqXbSvBAh/kPTHiWPAe/e1ODXo54DFMCbLQ1Zxn//o72e5Ddy5KO2iC/GdYUX58fN7Ob5olFkLTmXHUXSKUGkrTNeDgyojgnNh/vzBJGP1zKI5BN6K6bLp5mvXEDm/IbTD6K31e9brt8TbYgpswcbxJfm1Y0vkV0SI6RbuaQx3ww3HWsrh/WhG8fC6w/8k1gbgDF/3+m6wtdA50OncxwLf3aYrUX1e3VlwBnSwWoKbN1A2XSQjigws0cNOp8qe+ulyqpLCuMJbezN/P9hLn0pT0q9+LqR//+6CBfTObNNwjAiCNvYIA2gqxbB0zKuxXUtctY6BRfNLIdN2mtyIYC5irjsMJfBlKeMX3zTiJdvirwYOgdXBxpiU4MZkFhWBWYvk5hsh7OSelbd4bwi3uZLPA+nJZ7fNqLt27I6EYticCi2bJTghlmV5CxMm6Tpovkj29F5xdVpt9bMfdeIl+/K6mTZlmUxE1GTgcGzV6JO152XiprA9414+b5CX0BJDEs28lkUVRZqlmblUl7mM3IqbCFXiLT6msEPjUj7oaxMNsbUBNqQYTPK8Up9U3PWrgYvFTHDj414+bGsTMziEC4wCkky4shcBS3IwLmQIfl8xYm5mQuyD8vEPG9EzPPfiFmg0GaXChnj4oXmueJIhDLNjrSTwO8BZn4stB0nciPVDzB7rm1fw1xbljtYulC3UOKobyuYmF+fLppfrxi7Cw/N08l/zBeajEVGTv7OB9p5sqi2QbEMTjEZnmkl9ArtXk3fCcgLKTT1qJbvXGlmUrPPhPVqt2bfaaDuSddiuSDCo80GaNPV75PguX258GRCWdW9iy9lQbI1N3Z5t/1+EDtx0W/fUn77xdfKcd8uOe5bqtDdbOuGiz+ai6C5N8OY1ICNdAi4IXW1OSEUI2u83olzyimSjQcEYU7MRTCuCo1SiG8rhHN45kOknxqFSD9NrXctngn6S613XbAzmrNsHCLJCdCFKlrVSjDmRCnDt1OUQf2eQyHSP1wbpbB0ZBOTy6VlxETpmgS5AsWgPCnAUdtijOPl60Qe8bxuXMCb14+fG+nHz9MKWJa9Cv1YRgFrVeoxQ243ST9SXpSOfD+TjizgPAonWBudobpNwM5CbsAQNaiFx+tmCbZtSi25ppaxhVbWT1CZLAlValPvXn5ppD6/TC1Z8VW6l0VKVuvpXQr0KC36sU6L9ppozN76aAfRCzkzHseu+XbUhTZnmaofle5lr4Ty//7VRCdgdDnksrlp2iYn3DJtPtomcLk6sZyy1GVqRU1dIL80aE94be1NbcdzBvACqgO/98Jfn/ujtq4G5YJpy3+mlQsqUF9VuYCiQvuVVA+mz1UtKJaa/NWUmpZWTLnIoKmlNjEgyF6o1JRfFPXMjaJmdaZpa5jWSHDSrVQ2uE7zfT/1rVcTfMZ761xaarAP1SrqSneuFzZowS0nHyabIRbc7XvKtd4p+dTBZJeqdlYcIzlY8o6TK129O94ylaeANlugm9n1Np2C6ICKi8h1/JLKJ0btvcm8JEt0vdqa3qAuNZsjGVufABMtTaxr4csHj2UY7zYB8O4aQVdTAjWLJdAVoppNX2sFdClVtnUT3OpaGy/W2laB/e06vG83x/j2bLjWtAdPqB4vBO3lmISq3LIM6n4TOPfXR0BrClvmMgtbdQDv1YG511xC99ZN8+tqIlJacz90EWgPIAQpopq1thnnn0O4PxlbGdmMMetfpWhtg+iMYRMRbloWZEkGurWRtnZYBeDVSnqrwMeytjis5+zQDcNSZH1X8dUvxx3NdeHuuulCKQZJN9eGsI5A9MEsjiAWsUxiL6ILlbhWRQc1SB80wfhgfdAtxhijOW5pgRgxqGEyUANKF7LhleDu10G531xo99dNaIuekY1llnETLAsc5aZJ6aqmSdMq9vgDTnOQfC37g8kYF2rZH0xtH1h83UXQKAB8+aXsOXtf71bwU5PJ5Bn7sBFjH06d0K7aN2Nhxq74hPaMU0UVFO6XCfuoEWEfXcIU6gQVW8cp1DkJ26+gZ69Oqz5uRNLHlzCnV0HS1ZvTm8EO1qpSXe7xv08acfXJVJ+1+LKAV8RnHVTFFHUsfdqIpU+n+Slz8carV8NP7dcq1EGZpM8akfTZVN/0m2uaiaO9+vihro/x82n9cMUN09L2t0lO6tXzUTPwVb0t8UxVsSeTGSpuUfxkyf9RwcwcXd+q2WVuWZzfARZraWsSHjUn4bQ9CY8blAhv1qA0bXfYaX0mq6O+okGJjctG2JyxuaTYiRSsphNpae022U4kVY6HyKQepuyD38j+77Ty8+h/pH7n/1BLBwiiOmLODQ8AAMN6AABQSwECFAAUAAgACADbgPY8ojpizg0PAADDegAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAEcPAAAAAA==" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| + | |||
=Geogebra= | =Geogebra= | ||
| + | ==Thales== | ||
| + | Die Datei aus der Sitzung vom 8.Juni zum entdecken des Thalessatzes:<br /> | ||
| + | [https://www.geogebra.org/classic/trxxxsuv Thalessatz entdecken 8. Juni 2020 Leitideen II] | ||
| + | ==Satz über die gegenüberliegenden Winkel im Sehnenviereck== | ||
| + | Die Datei aus der Sitzung vom 8. Juni 2020<br /> | ||
| + | [https://www.geogebra.org/classic/q4hr4mqw Sehnenviereckssatz entdecken 8. Juni 2020] | ||
==Höhensatz== | ==Höhensatz== | ||
| − | Die Datei aus der Sitzung vom 8.Juni zum Entdecken des Höhensatzes<br /> | + | Die Datei aus der Sitzung vom 8.Juni zum Entdecken des Höhensatzes:<br /> |
[https://www.geogebra.org/classic/butjskkr Höhensatz mit Geogebra entdecken] | [https://www.geogebra.org/classic/butjskkr Höhensatz mit Geogebra entdecken] | ||
Aktuelle Version vom 8. Juni 2020, 13:23 Uhr
Inhaltsverzeichnis |
Das Whiteboard der Sitzungen vom 25. Mai und vom 8. Juni zur Satzfindung
Den Satz über die gegenüberliegenden Winkel im Sehnenviereck entdecken
Video
[ www.youtube.com is not an authorized iframe site ]
Das Wesentliche des Videos
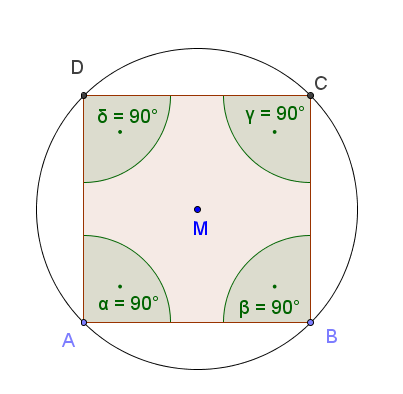
sehr speziell: Quadrate
Jedes Quadrat hat einen Umkreis und ist somit ein Sehnenviereck.
weniger speziell, aber immer noch ziemlich speziell: Rechtecke
Jedes Rechteck ist ein Sehnenviereck.
noch allgemeiner, aber immer noch ziemlich speziell: gleichschenklige Trapeze
Jedes gleichschenklige Trapez ist ein Sehnenviereck.
allgemeines Sehnenviereck
Ausgangslage: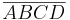 
ist ein gleichschenkliges Trapez.
Arbeitsauftrag: Bewegen Sie den Punkt 
auf dem Kreis. Beobachten Sie, wie sich der rote und der blaue Winkel verändern. Was vermuten Sie bezüglich der Größe von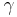 
? Was vermuten Sie hinsichtlich der Größen der gegenüberliegenden Winkel im Sehnenviereck?
Der Satz über die gegenüberliegenden Winkel im Sehnenviereck
Geogebra
Thales
Die Datei aus der Sitzung vom 8.Juni zum entdecken des Thalessatzes:
Thalessatz entdecken 8. Juni 2020 Leitideen II
Satz über die gegenüberliegenden Winkel im Sehnenviereck
Die Datei aus der Sitzung vom 8. Juni 2020
Sehnenviereckssatz entdecken 8. Juni 2020
Höhensatz
Die Datei aus der Sitzung vom 8.Juni zum Entdecken des Höhensatzes:
