Lösung von Aufg. 6.1P (SoSe 20): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
Es seien eine Gerade g und zwei Punkte A und B, wobei A,B Elemente von g sind. A teilt g in zwei Halbgeraden. Die Halbgerade, die B nicht enthält ist die Halbgerade <math>\ AB^-</math>.--[[Benutzer:Kohlhoffj|tgksope]] ([[Benutzer Diskussion:Kohlhoffj|Diskussion]]) 17:05, 22. Jul. 2020 (CEST) | Es seien eine Gerade g und zwei Punkte A und B, wobei A,B Elemente von g sind. A teilt g in zwei Halbgeraden. Die Halbgerade, die B nicht enthält ist die Halbgerade <math>\ AB^-</math>.--[[Benutzer:Kohlhoffj|tgksope]] ([[Benutzer Diskussion:Kohlhoffj|Diskussion]]) 17:05, 22. Jul. 2020 (CEST) | ||
| + | |||
| + | Mathematisch könnte es so heißen: <math>\ AB^- = \mathcal{f} P \mid A \in \overline { PB } \mathcal{g}</math> --[[Benutzer:Tutorin Laura|Tutorin Laura]] ([[Benutzer Diskussion:Tutorin Laura|Diskussion]]) 18:58, 23. Jul. 2020 (CEST) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Aktuelle Version vom 23. Juli 2020, 17:58 Uhr
Geben Sie eine formal korrekte Definition für die Halbgerade 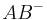 an, ohne die Zwischenrelation zu verwenden.
an, ohne die Zwischenrelation zu verwenden.
Es seien eine Gerade g und zwei Punkte A und B, wobei A,B Elemente von g sind. A teilt g in zwei Halbgeraden. Die Halbgerade, die B nicht enthält ist die Halbgerade 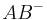 .--tgksope (Diskussion) 17:05, 22. Jul. 2020 (CEST)
.--tgksope (Diskussion) 17:05, 22. Jul. 2020 (CEST)
Mathematisch könnte es so heißen:--Tutorin Laura (Diskussion) 18:58, 23. Jul. 2020 (CEST)

