Lösung von Aufg. 6.2P (WS 20 21): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 4: | Zeile 4: | ||
...<math>M= \big\{P| \forall A,B \in M \wedge Zw(A,P,B): P \in M \big\} </math>--[[Benutzer:Werzdavid|Werzdavid]] ([[Benutzer Diskussion:Werzdavid|Diskussion]]) 09:34, 10. Dez. 2020 (CET) | ...<math>M= \big\{P| \forall A,B \in M \wedge Zw(A,P,B): P \in M \big\} </math>--[[Benutzer:Werzdavid|Werzdavid]] ([[Benutzer Diskussion:Werzdavid|Diskussion]]) 09:34, 10. Dez. 2020 (CET) | ||
| − | P ist | + | Was genau stellt das P dar? |
| − | + | Deine Definition ist nicht falsch, aber du kannst sie einfacher und ohne die Zwischenrelation aufstellen. | |
<u>Tipp:</u> | <u>Tipp:</u> | ||
M ist konvex, wenn gilt: '''Für alle A, B Element der Menge M => Die gesamte Strecke von A und B gehört zur Menge M.''' | M ist konvex, wenn gilt: '''Für alle A, B Element der Menge M => Die gesamte Strecke von A und B gehört zur Menge M.''' | ||
Aktuelle Version vom 12. Dezember 2020, 11:22 Uhr
Definieren Sie den Begriff: "konvexe Punktmenge" indem Sie die verbal formulierte Definition (siehe Wiki-Skript) in eine geeignete "Mengenschreibweise" übersetzen.
M ist konvex, wenn gilt: ...
...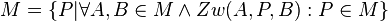 --Werzdavid (Diskussion) 09:34, 10. Dez. 2020 (CET)
--Werzdavid (Diskussion) 09:34, 10. Dez. 2020 (CET)
Was genau stellt das P dar? Deine Definition ist nicht falsch, aber du kannst sie einfacher und ohne die Zwischenrelation aufstellen. Tipp: M ist konvex, wenn gilt: Für alle A, B Element der Menge M => Die gesamte Strecke von A und B gehört zur Menge M. Du musst jetzt quasi nur noch das Fettgedruckte in mathematische Schreibweise umwandeln. --Tutorin Laura (Diskussion) 11:21, 12. Dez. 2020 (CET)

