Lösung von Aufgabe 5.5 P (SoSe 22): Unterschied zwischen den Versionen
Kwd077 (Diskussion | Beiträge) |
|||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
transitiv: ist nur dann nicht der Fall, wenn eine dritte Gerade i die Gerade h schneidet, aber die Gerade g nicht schneidet, also wenn gilt : | transitiv: ist nur dann nicht der Fall, wenn eine dritte Gerade i die Gerade h schneidet, aber die Gerade g nicht schneidet, also wenn gilt : | ||
g schneidet h, h schneidet i und g schneidet nicht i, dann ist sie nicht transitiv--[[Benutzer:Kwd077|Kwd077]] ([[Benutzer Diskussion:Kwd077|Diskussion]]) 16:05, 16. Mai 2022 (CEST) | g schneidet h, h schneidet i und g schneidet nicht i, dann ist sie nicht transitiv--[[Benutzer:Kwd077|Kwd077]] ([[Benutzer Diskussion:Kwd077|Diskussion]]) 16:05, 16. Mai 2022 (CEST) | ||
| + | |||
| + | Beachte: eine Relation ist nur dann transitiv wenn für ALLE Elemente der Relation gilt: Wenn aRb und bRc dann gilt aRc. | ||
| + | --[[Benutzer:Matze2000|Matze2000]] ([[Benutzer Diskussion:Matze2000|Diskussion]]) 15:18, 19. Mai 2022 (CEST) | ||
Aktuelle Version vom 19. Mai 2022, 14:18 Uhr
Untersuchen Sie folgende Relation S auf ihre Eigenschaften:
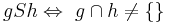
reflexiv ja, da die Gerade g geschnitten mit sich selbst die Gerade g ergibt, daher gibt es keine leere Menge symmetrisch ja, weil die Gerade g geschnitten mit der Geraden h und die Gerade h geschnitten mit der Geraden g keine leere Menge ergibt transitiv: ist nur dann nicht der Fall, wenn eine dritte Gerade i die Gerade h schneidet, aber die Gerade g nicht schneidet, also wenn gilt : g schneidet h, h schneidet i und g schneidet nicht i, dann ist sie nicht transitiv--Kwd077 (Diskussion) 16:05, 16. Mai 2022 (CEST)
Beachte: eine Relation ist nur dann transitiv wenn für ALLE Elemente der Relation gilt: Wenn aRb und bRc dann gilt aRc. --Matze2000 (Diskussion) 15:18, 19. Mai 2022 (CEST)

