Lösung von Aufgabe 10.2P (SoSe 22): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Beweisen Sie Satz IX.2:<br /> Gegeben seien zwei Spiegelgeraden ''a'' und ''b'' mit einem gemeinsamen Schnittpunkt ''S'', sowie zwei Punkten <math>A\in a</math…“) |
Kwd077 (Diskussion | Beiträge) |
||
| Zeile 6: | Zeile 6: | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
| + | Beweis: ein Versuch | ||
| + | |||
| + | Vor: P``= Sa verkettet mit Sb(P) mit S = a schneidet b, A Element a. B Element b, A und B sind ungleich S | ||
| + | Beh: Winkel PSP``= 2* Winkel ASB | ||
| + | |||
| + | Beweis: | ||
| + | 1. S Element a und S Element b, Begründung: Vor | ||
| + | 2. A Element a und B Element b, A und B ungleich S, Begründung: Vor | ||
| + | 3. P Element Halbebene a+, Begründung: Vor., Def. Halbebene | ||
| + | 4. P``ist Bildpunkt von P, Begründung: 1., 2., 3., Def. Verkettung von Abbildungen | ||
| + | 5. Abstand SP ist gleich dem Abstand SP``, Begründung: 4., Def. Verkettung von Abb., Satz IX.1: jeder Punkt P liegt mit seinem Bildpunkt P``= Sa verkettet SB(P) um einen Kreis K um S | ||
| + | 6. Strecke SP sowie Strecke SP``= Radius von K, Begründung: 5., Streckentreue, | ||
| + | 7. Winkel PSP``= 180 Grad, Begründung: 4., 5., 6., Def. Winkel: ein Winkel besteht aus zwei Strahlen SP+ und SP``+, Scheitelpunkt des Winkels ist S | ||
| + | 8. Winkel ASB + Winkel ASB`= 180 Grad, Begründung: 1., 2., Definition Supplementärwinkel: Winkel heißen supplementär, wenn sie zusammen 180 Grad ergeben | ||
| + | 9. Winkel ASB = 90 Grad, Begründung: 8., Def. Punktspiegelung und Geradenspiegelung | ||
| + | 10. Winkel PSP``= 2* Winkel ASB, Begründung: 9., Definition Drehung : eine Drehung ist eine Verkettung zweier Geradenspiegelungen mit S als Schnittpunkt | ||
| + | 11. Behauptung stimmt--[[Benutzer:Kwd077|Kwd077]] ([[Benutzer Diskussion:Kwd077|Diskussion]]) 12:29, 27. Jun. 2022 (CEST) | ||
Aktuelle Version vom 27. Juni 2022, 11:29 Uhr
Beweisen Sie Satz IX.2:
Gegeben seien zwei Spiegelgeraden a und b mit einem gemeinsamen Schnittpunkt S, sowie zwei Punkten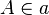 
und 
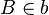, die von S jeweils verschieden sind. Wir betrachten die Verkettung 
. Für einen beliebigen Punkt P und seinen Bildpunkt 
gilt: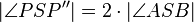 
.
Beweis: ein Versuch
Vor: P``= Sa verkettet mit Sb(P) mit S = a schneidet b, A Element a. B Element b, A und B sind ungleich S Beh: Winkel PSP``= 2* Winkel ASB
Beweis: 1. S Element a und S Element b, Begründung: Vor 2. A Element a und B Element b, A und B ungleich S, Begründung: Vor 3. P Element Halbebene a+, Begründung: Vor., Def. Halbebene 4. P``ist Bildpunkt von P, Begründung: 1., 2., 3., Def. Verkettung von Abbildungen 5. Abstand SP ist gleich dem Abstand SP``, Begründung: 4., Def. Verkettung von Abb., Satz IX.1: jeder Punkt P liegt mit seinem Bildpunkt P``= Sa verkettet SB(P) um einen Kreis K um S 6. Strecke SP sowie Strecke SP``= Radius von K, Begründung: 5., Streckentreue, 7. Winkel PSP``= 180 Grad, Begründung: 4., 5., 6., Def. Winkel: ein Winkel besteht aus zwei Strahlen SP+ und SP``+, Scheitelpunkt des Winkels ist S 8. Winkel ASB + Winkel ASB`= 180 Grad, Begründung: 1., 2., Definition Supplementärwinkel: Winkel heißen supplementär, wenn sie zusammen 180 Grad ergeben 9. Winkel ASB = 90 Grad, Begründung: 8., Def. Punktspiegelung und Geradenspiegelung 10. Winkel PSP``= 2* Winkel ASB, Begründung: 9., Definition Drehung : eine Drehung ist eine Verkettung zweier Geradenspiegelungen mit S als Schnittpunkt 11. Behauptung stimmt--Kwd077 (Diskussion) 12:29, 27. Jun. 2022 (CEST)
