Lösung von Aufgabe 13.2P (SoSe 22): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Dargestellt ist hier die Nacheinanderausführung zweier Abbildungen <math> \varphi_{1} , \varphi _{2} </math>, mit <math> \triangle \overline{a'b'c'} = \va…“)
 
 
(Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt)
Zeile 13: Zeile 13:
  
 
[[Kategorie:Geo_P]]
 
[[Kategorie:Geo_P]]
 +
1.- Geradenspiegleung
 +
  - Schubspiegelung
 +
3.  1) Sa ° Sb ° Sc ° Sd = Sa` ° Sb ° Sc ° Sd mit a` parallel zu b und d, und a` senkrecht zu d, eigenschaft Drehung
 +
    2) Sa`° Sb ° Sc ° Sd = Sa``° Sb` ° Sc ° Sd mit a`` parallel zu b`, a`` senkrecht zu d,  a`` schneidet d im Punkt D, b`= c--> Identität, Abstand
 +
      a``zu b` ist gleich dem Abstand a` zu b, Eigenschaft Verschiebung
 +
    3 ) Sa`` ° Sd => Punktspiegelung um D um 180 grad --[[Benutzer:Kwd077|Kwd077]] ([[Benutzer Diskussion:Kwd077|Diskussion]]) 11:34, 18. Jul. 2022 (CEST)
 +
 +
Die Begründung musst du dir nochmal anschauen. Denke dabei an die Reihenfolge der Geraden. Wenn du eine Drehung "drehst" müssen beide Achsen weiterhin einen gleichgroßen Winkel zueinander haben.--[[Benutzer:Matze2000|Matze2000]] ([[Benutzer Diskussion:Matze2000|Diskussion]]) 18:15, 21. Jul. 2022 (CEST)

Aktuelle Version vom 21. Juli 2022, 17:15 Uhr

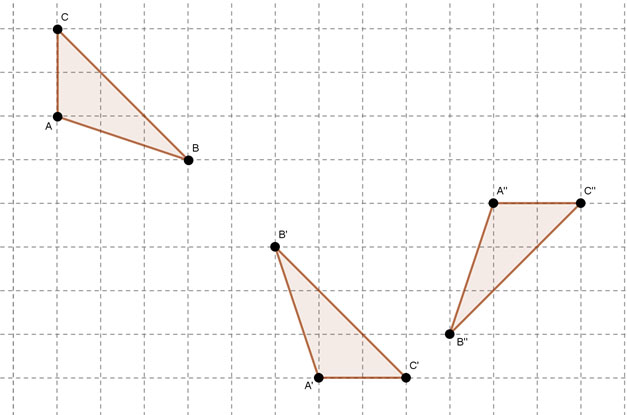
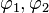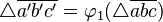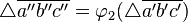Dargestellt ist hier die Nacheinanderausführung zweier Abbildungen \varphi_{1} , \varphi _{2} , mit \triangle \overline{a'b'c'} = \varphi _{1}( \triangle \overline{abc}) und \triangle \overline{a''b''c''} = \varphi _{2}( \triangle \overline{a'b'c'}) .

Verkettung 13 2.jpg

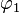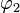  1. wie heißen die beiden Abbildungen \varphi_{1} und \varphi _{2} ?
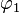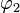  2. Zeichnen Sie jeweils für \varphi_{1} und \varphi _{2} die passende Anzahl von Spiegelachsen in die Skizze ein.
  3. Durch welche Ersatzabbildung kann die Verkettung 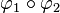\varphi_{1} \circ \varphi _{2} ersetzt werden (Begründen Sie Ihre Entscheidung)?
  4. Zeichnen Sie die Achsen der Ersatzabbildung in die Skizze ein.

1.- Geradenspiegleung 

 - Schubspiegelung

3. 1) Sa ° Sb ° Sc ° Sd = Sa` ° Sb ° Sc ° Sd mit a` parallel zu b und d, und a` senkrecht zu d, eigenschaft Drehung 

   2) Sa`° Sb ° Sc ° Sd = Sa``° Sb` ° Sc ° Sd mit a`` parallel zu b`, a`` senkrecht zu d,  a`` schneidet d im Punkt D, b`= c--> Identität, Abstand 
     a``zu b` ist gleich dem Abstand a` zu b, Eigenschaft Verschiebung
   3 ) Sa`` ° Sd => Punktspiegelung um D um 180 grad --Kwd077 (Diskussion) 11:34, 18. Jul. 2022 (CEST)

Die Begründung musst du dir nochmal anschauen. Denke dabei an die Reihenfolge der Geraden. Wenn du eine Drehung "drehst" müssen beide Achsen weiterhin einen gleichgroßen Winkel zueinander haben.--Matze2000 (Diskussion) 18:15, 21. Jul. 2022 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_13.2P_(SoSe_22)&oldid=38404“