Satz des Pythagoras WS 23 24: Unterschied zwischen den Versionen
(→Erinnerung: Rechtwinklige Dreiecke) |
|||
| (31 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<br />Falls nichts angezeigt wird, können Sie mit folgendem Link [{{fullurl:{{PAGENAME}}|action=purge}} den Servercache leeren]. | <br />Falls nichts angezeigt wird, können Sie mit folgendem Link [{{fullurl:{{PAGENAME}}|action=purge}} den Servercache leeren]. | ||
| + | == '''Die Länge der Bildschirmdiagonale...''' == | ||
| − | + | Hans möchte seinen alten Laptop verkaufen. Im Verkaufsportal muss er die Länge der Bildschirmdiagonale angeben. Bisher weiß er nur, dass der Bildschirm 25cm lang und 17cm breit ist. | |
| − | |||
| − | + | '''Frage:''' '''Wie kann er die Länge der Bildschirmdiagonale berechnen?''' | |
| − | |||
| − | |||
| − | + | Schau dir die Situation auf dem Bild noch einmal genau an. | |
| − | + | Welche geometrische Figur erkennst du? | |
| − | + | [[Datei:Hans.png|miniatur|zentriert]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| + | Du hast ein rechtwinkliges Dreieck erkannt? Sehr gut! | ||
== '''Erinnerung: Rechtwinklige Dreiecke''' == | == '''Erinnerung: Rechtwinklige Dreiecke''' == | ||
| − | + | Ein rechtwinkliges Dreieck hat immer '''zwei Katheten''' und '''eine Hypotenuse'''. | |
| − | + | Die '''Hypotenuse''' ist die längste Seite und liegt immer gegenüber vom '''rechten Winkel'''. | |
| − | Ein rechtwinkliges Dreieck hat immer '''zwei Katheten''' und '''eine | + | |
| − | Die ''' | + | |
Die anderen beiden Seiten sind die '''Katheten'''. | Die anderen beiden Seiten sind die '''Katheten'''. | ||
| + | |||
| + | [[Datei:Das rechtwinklige Dreieck.png|miniatur|zentriert]] | ||
Damit du die Abbildung besser erkennen kannst, klicke auf das Symbol mit den zwei kleinen Rechtecken am rechten unteren Rand der Abbildung. | Damit du die Abbildung besser erkennen kannst, klicke auf das Symbol mit den zwei kleinen Rechtecken am rechten unteren Rand der Abbildung. | ||
| − | == ''' | + | == '''Hinführung zum Satz des Pythagoras''' == |
| − | + | Hans schildert sein Problem seiner Mathelehrerin. Sie meint, er könne das Problem mit dem '''Satz des Pythagoras''' lösen. | |
| − | a) Bewege nun | + | |
| − | + | '''Frage: Was ist der Satz des Pythagoras?!''' | |
| + | |||
| + | |||
| + | In der Abbildung unten siehst du das '''rechtwinklige Dreieck ABC''' mit den '''Seiten a, b und c'''. Die Flächen <math>a^{2}</math>, <math>b^{2}</math> und <math>c_{1} ^{2}</math> wurden aus dem Quadrat der jeweiligen Seiten gebildet (z.B. Seite a: a*a = <math>a^{2}</math> = blaue Fläche). Die Flächen sind deshalb '''quadratisch'''. | ||
| + | |||
| + | |||
| + | a) Bewege nun den '''Punkt C'''. Wie verändern sich die Flächen '''<math>a^{2}</math>, <math>b^{2}</math> und <math>c_{1} ^{2}</math>'''? Besprich dich mit deinem Sitznachbarn/deiner Sitznachbarin. | ||
<ggb_applet id="fjwqbwgn" width="1320" height="798" border="888888" /> | <ggb_applet id="fjwqbwgn" width="1320" height="798" border="888888" /> | ||
| − | Haltet eure Beobachtungen schriftlich fest, indem ihr die folgenden Aussagen mit '''„wahr“''' oder '''„falsch“''' bewertet. | + | b) Haltet eure Beobachtungen schriftlich fest, indem ihr die folgenden Aussagen mit '''„wahr“''' oder '''„falsch“''' bewertet. |
{| class="wikitable" | {| class="wikitable" | ||
| Zeile 55: | Zeile 57: | ||
| − | + | c) Gut beobachtet! Die Größe der Fläche <math>c_{1} ^{2}</math> verändert sich nicht. Beobachte nun den Wert der Fläche des grünen Quadrates (<math>b^{2}</math>) und den der Fläche des blauen Quadrates (<math>a^{2}</math>). Erkennst du einen Zusammenhang zwischen den Werten dieser beiden Flächen und dem Wert der Fläche des roten Quadrates (<math>c_{1} ^{2}</math>)? | |
| − | + | <ggb_applet id="dgbg4ung" width="1354" height="735" border="888888" /> | |
| + | |||
| + | == '''Der Satz des Pythagoras''' == | ||
| + | |||
| + | Diese Beobachtung hat schon der Mathematiker und Philosoph '''Pythagoras von Samos''' zwischen 580 und 500 v.Chr. festgehalten! | ||
| + | [[Datei:Pythagoras 1.png|miniatur|zentriert]] | ||
'''Der Satz des Pythagoras:''' | '''Der Satz des Pythagoras:''' | ||
| Zeile 64: | Zeile 71: | ||
Daher gilt: '''<math>a^{2}</math> + <math>b^{2}</math> = <math>c^{2}</math>''' | Daher gilt: '''<math>a^{2}</math> + <math>b^{2}</math> = <math>c^{2}</math>''' | ||
| − | Die Summe der Flächen der Katheten (in unserem Dreieck also <math>a^{2}</math> + <math>b^{2}</math>) ist also immer genauso groß, wie die Fläche der | + | Die Summe der Flächen der Katheten (in unserem Dreieck also <math>a^{2}</math> + <math>b^{2}</math>) ist also immer genauso groß, wie die Fläche der Hypotenuse (in unserem Beispiel <math>c_{1} ^{2}</math>). Ganz egal, ob <math>a^{2}</math> kleiner als <math>b^{2}</math> ist, oder andersherum. |
| + | |||
| + | == '''Berechnung der Länge der Bildschirmdiagonale''' == | ||
| + | |||
| + | Wende nun den Satz des Pythagoras an, um die Länge der Bildschirmdiagonale von Hans' Laptop zu berechnen. Schreibe die Rechnung in dein Heft. Versuche zunächst, die Rechnung selbstständig aufzustellen. Wenn du nicht weiterkommst, darfst du die Tipps verwenden. | ||
| + | |||
| + | <ggb_applet id="nr6c5bfg" width="1355" height="736" border="888888" /> | ||
| + | |||
| + | == '''Übung''' == | ||
| − | Verzaubert von der Magie des Satz des Pythagoras? Dann stürze dich in die Übungsaufgaben | + | Verzaubert von der Magie des Satz des Pythagoras? Dann stürze dich in die Übungsaufgaben der [https://learningapps.org/watch?v=py90a17u524 LearningApp]! Viel Erfolg! :) |
Aktuelle Version vom 16. Februar 2024, 11:40 Uhr
Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren.
Inhaltsverzeichnis |
Die Länge der Bildschirmdiagonale...
Hans möchte seinen alten Laptop verkaufen. Im Verkaufsportal muss er die Länge der Bildschirmdiagonale angeben. Bisher weiß er nur, dass der Bildschirm 25cm lang und 17cm breit ist.
Frage: Wie kann er die Länge der Bildschirmdiagonale berechnen?
Schau dir die Situation auf dem Bild noch einmal genau an.
Welche geometrische Figur erkennst du?
Du hast ein rechtwinkliges Dreieck erkannt? Sehr gut!
Erinnerung: Rechtwinklige Dreiecke
Ein rechtwinkliges Dreieck hat immer zwei Katheten und eine Hypotenuse. Die Hypotenuse ist die längste Seite und liegt immer gegenüber vom rechten Winkel. Die anderen beiden Seiten sind die Katheten.
Damit du die Abbildung besser erkennen kannst, klicke auf das Symbol mit den zwei kleinen Rechtecken am rechten unteren Rand der Abbildung.
Hinführung zum Satz des Pythagoras
Hans schildert sein Problem seiner Mathelehrerin. Sie meint, er könne das Problem mit dem Satz des Pythagoras lösen.
Frage: Was ist der Satz des Pythagoras?!
In der Abbildung unten siehst du das rechtwinklige Dreieck ABC mit den Seiten a, b und c. Die Flächen 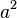 ,
, 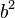 und
und 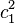 wurden aus dem Quadrat der jeweiligen Seiten gebildet (z.B. Seite a: a*a =
wurden aus dem Quadrat der jeweiligen Seiten gebildet (z.B. Seite a: a*a = 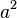 = blaue Fläche). Die Flächen sind deshalb quadratisch.
= blaue Fläche). Die Flächen sind deshalb quadratisch.
a) Bewege nun den Punkt C. Wie verändern sich die Flächen 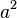 ,
, 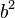 und
und 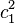 ? Besprich dich mit deinem Sitznachbarn/deiner Sitznachbarin.
? Besprich dich mit deinem Sitznachbarn/deiner Sitznachbarin.
b) Haltet eure Beobachtungen schriftlich fest, indem ihr die folgenden Aussagen mit „wahr“ oder „falsch“ bewertet.
| Aussage | wahr | falsch |
|---|---|---|
Wenn man den Punkt C bewegt, dann verändert sich die Größe der Fläche 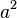 . . |
||
Wenn man den Punkt C bewegt, dann verändert sich die Größe der Fläche 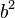 . . |
||
Wenn man den Punkt C bewegt, dann verändert sich die Größe der Fläche 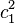 . . |
c) Gut beobachtet! Die Größe der Fläche 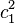 verändert sich nicht. Beobachte nun den Wert der Fläche des grünen Quadrates (
verändert sich nicht. Beobachte nun den Wert der Fläche des grünen Quadrates (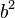 ) und den der Fläche des blauen Quadrates (
) und den der Fläche des blauen Quadrates (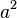 ). Erkennst du einen Zusammenhang zwischen den Werten dieser beiden Flächen und dem Wert der Fläche des roten Quadrates (
). Erkennst du einen Zusammenhang zwischen den Werten dieser beiden Flächen und dem Wert der Fläche des roten Quadrates (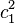 )?
)?
Der Satz des Pythagoras
Diese Beobachtung hat schon der Mathematiker und Philosoph Pythagoras von Samos zwischen 580 und 500 v.Chr. festgehalten!
Der Satz des Pythagoras: In einem rechtwinkligen Dreieck ist die Summe der Quadrate der Katheten genauso groß wie das Quadrat der Hypotenuse.
Daher gilt: 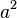 +
+ 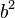 =
= 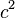
Die Summe der Flächen der Katheten (in unserem Dreieck also 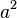 +
+ 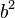 ) ist also immer genauso groß, wie die Fläche der Hypotenuse (in unserem Beispiel
) ist also immer genauso groß, wie die Fläche der Hypotenuse (in unserem Beispiel 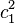 ). Ganz egal, ob
). Ganz egal, ob 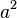 kleiner als
kleiner als 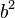 ist, oder andersherum.
ist, oder andersherum.
Berechnung der Länge der Bildschirmdiagonale
Wende nun den Satz des Pythagoras an, um die Länge der Bildschirmdiagonale von Hans' Laptop zu berechnen. Schreibe die Rechnung in dein Heft. Versuche zunächst, die Rechnung selbstständig aufzustellen. Wenn du nicht weiterkommst, darfst du die Tipps verwenden.
Übung
Verzaubert von der Magie des Satz des Pythagoras? Dann stürze dich in die Übungsaufgaben der LearningApp! Viel Erfolg! :)




