Lösung von Aufgabe 4.4: Unterschied zwischen den Versionen
| (8 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:<br /> | Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:<br /> | ||
Es seien ''a'', ''b'' und ''c'' drei paarweise verschiedene Geraden in ein und derselben Ebene.<br /> | Es seien ''a'', ''b'' und ''c'' drei paarweise verschiedene Geraden in ein und derselben Ebene.<br /> | ||
| − | a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: <math>\ a \| b \land | + | a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: <math>\ a \| b \land b \| c \Rightarrow \ a \| c</math> . <br /> |
b) Welche Eigenschaft der Relation <math>\| </math> auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?<br /> | b) Welche Eigenschaft der Relation <math>\| </math> auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?<br /> | ||
VSS: a//b und b//c<br /> | VSS: a//b und b//c<br /> | ||
| Zeile 15: | Zeile 15: | ||
Annahme ist zu verwerfen<br /> | Annahme ist zu verwerfen<br /> | ||
daraus folgt a//c<br /> | daraus folgt a//c<br /> | ||
| − | b) Transitivität<br />--[[Benutzer:Engel82|Engel82]] 12:42, 4. Nov. 2010 (UTC) | + | b) Transitivität<br />--[[Benutzer:Engel82|Engel82]] 12:42, 4. Nov. 2010 (UTC)<br /> |
| + | Die Lösung von Engel82 ist korrekt!--[[Benutzer:Schnirch|Schnirch]] 13:59, 24. Nov. 2010 (UTC) | ||
| − | Was bedeutet das "S e c" und "S e a"? | + | Was bedeutet das "S e c" und "S e a"? <br /> |
| − | + | --> ich denke man meint mit S den Schnittpunkt und mit e Element, also S ist Element von a. --[[Benutzer:Kinder Riegel|Kinder Riegel]] 02:51, 9. Nov. 2010 (UTC)<br /> | |
| + | |||
| + | Und woher das "b//c" in der Aufgabenstellung gibt es das nicht | ||
| + | |||
| + | das b//c gehört in die Aufgabenstellung. da hat sich ein kleiner Fehler eingeschlichen. warum sollte in Implikation und Behauptung das selbe stehen.--[[Benutzer:Sommer80|Sommer80]] 10:42, 9. Nov. 2010 (UTC) <- Das ist doch Mathe? Jeder Nonsense ist möglich! | ||
| + | Sommer80 hat Recht, ich habe den Fehler korrigiert, Danke für den Hinweis!--[[Benutzer:Schnirch|Schnirch]] 13:59, 24. Nov. 2010 (UTC) | ||
| + | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 24. November 2010, 14:59 Uhr
Das Parallelenaxiom lautet wie folgt:
Zu jeder Geraden g und zu jedem nicht auf g liegenden Punkt A gibt es höchstens eine Gerade, die durch A verläuft und zu g parallel ist.
Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:
Es seien a, b und c drei paarweise verschiedene Geraden in ein und derselben Ebene.
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: 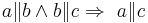 .
.
b) Welche Eigenschaft der Relation 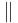 auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
VSS: a//b und b//c
Beh: a//c
Annahme: a ist nicht parallel zu c
1. a geschnitten mit c hat den Schnittpunkt S_____nach Annhamne
2. a ist parallel zu b mit S e a und c ist parallel zu b mit S e c____1.
3. zu b existieren zwei verschiedene Parallelen a und c durch S___1. und 2.
4. Widerspruch zum Parallenaxiom
Annahme ist zu verwerfen
daraus folgt a//c
b) Transitivität
--Engel82 12:42, 4. Nov. 2010 (UTC)
Die Lösung von Engel82 ist korrekt!--Schnirch 13:59, 24. Nov. 2010 (UTC)
Was bedeutet das "S e c" und "S e a"?
--> ich denke man meint mit S den Schnittpunkt und mit e Element, also S ist Element von a. --Kinder Riegel 02:51, 9. Nov. 2010 (UTC)
Und woher das "b//c" in der Aufgabenstellung gibt es das nicht
das b//c gehört in die Aufgabenstellung. da hat sich ein kleiner Fehler eingeschlichen. warum sollte in Implikation und Behauptung das selbe stehen.--Sommer80 10:42, 9. Nov. 2010 (UTC) <- Das ist doch Mathe? Jeder Nonsense ist möglich!
Sommer80 hat Recht, ich habe den Fehler korrigiert, Danke für den Hinweis!--Schnirch 13:59, 24. Nov. 2010 (UTC)

