Lösung von Aufg. 6.2: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: Oberstudienrat Kramer beginnt die Stunde zur analytischen Geometrie mit der Frage, ob denn jemand wüsste, wie eine Gerade im <math>\mathbb{R}^2</math> definiert wäre....) |
|||
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Oberstudienrat Kramer beginnt die Stunde zur analytischen Geometrie mit der Frage, ob denn jemand wüsste, wie eine Gerade im <math>\mathbb{R}^2</math> definiert wäre. Vergleichen Sie mit Aufgabe 1. | + | --[[Benutzer:Sommer80|Sommer80]] 13:44, 17. Nov. 2010 (UTC)Oberstudienrat Kramer beginnt die Stunde zur analytischen Geometrie mit der Frage, ob denn jemand wüsste, wie eine Gerade im <math>\mathbb{R}^2</math> definiert wäre. Vergleichen Sie mit Aufgabe 1.<br /> |
| − | + | ||
| + | ==Lösung --[[Benutzer:Schnirch|Schnirch]] 13:10, 2. Dez. 2010 (UTC)== | ||
| + | Die analytische Geometrie kann als Modell der Euklidischen Geometrie betrachtet werden. Im Rahmen eines Modells können die darin vorkommenden Begriffe dann schon definiert werden. Geraden sind in diesem Modell in Form von Geradengleichungen definiert. <br />Man kann das vergleichen mit dem Tetraedermodell: Der Tetraeder mit seinen Ecken (Punkte), Kanten (Geraden) und Seitenflächen (Ebenen) ist ein gültiges Modell der Inzidenzgeometrie. Die Begriffe Ecken, Kanten und Seitenflächen lassen sich im Rahmen des Tetraedermodells exakt definieren.<br /> | ||
| + | Übrigens, lässt sich auch umgekehrt die analytische Geometrie axiomatisch aufbauen und die Euklidische Geometrie dann als Modell der analytischen Geometrie betrachten. | ||
| + | ==vorangegangene Diskussion== | ||
| + | Analog zu Aufgabe 1.<br /> | ||
| + | Man kann Geraden auch nicht in einer Ebene definieren, da Ebene und Geraden undefinierte Grundbergriffe sind.<br /> | ||
| + | Die Grundbegriffe kann man mit Inhalt aufgrund der Axiome füllen.<br />--[[Benutzer:Engel82|Engel82]] 13:08, 17. Nov. 2010 (UTC) | ||
| + | Ich war mir hier nicht sicher, aber ich glaube das hat was mit den vektoren zu tun und deswegen sind Geraden irgendwie definierbar in R2. Weiß aber nicht genau wie | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 2. Dezember 2010, 14:10 Uhr
--Sommer80 13:44, 17. Nov. 2010 (UTC)Oberstudienrat Kramer beginnt die Stunde zur analytischen Geometrie mit der Frage, ob denn jemand wüsste, wie eine Gerade im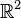 
definiert wäre. Vergleichen Sie mit Aufgabe 1.
Lösung --Schnirch 13:10, 2. Dez. 2010 (UTC)
Die analytische Geometrie kann als Modell der Euklidischen Geometrie betrachtet werden. Im Rahmen eines Modells können die darin vorkommenden Begriffe dann schon definiert werden. Geraden sind in diesem Modell in Form von Geradengleichungen definiert.
Man kann das vergleichen mit dem Tetraedermodell: Der Tetraeder mit seinen Ecken (Punkte), Kanten (Geraden) und Seitenflächen (Ebenen) ist ein gültiges Modell der Inzidenzgeometrie. Die Begriffe Ecken, Kanten und Seitenflächen lassen sich im Rahmen des Tetraedermodells exakt definieren.
Übrigens, lässt sich auch umgekehrt die analytische Geometrie axiomatisch aufbauen und die Euklidische Geometrie dann als Modell der analytischen Geometrie betrachten.
vorangegangene Diskussion
Analog zu Aufgabe 1.
Man kann Geraden auch nicht in einer Ebene definieren, da Ebene und Geraden undefinierte Grundbergriffe sind.
Die Grundbegriffe kann man mit Inhalt aufgrund der Axiome füllen.
--Engel82 13:08, 17. Nov. 2010 (UTC)
Ich war mir hier nicht sicher, aber ich glaube das hat was mit den vektoren zu tun und deswegen sind Geraden irgendwie definierbar in R2. Weiß aber nicht genau wie
