Lösung von Aufg. 8.5: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| (10 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex. | Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex. | ||
| + | == Lösung --[[Benutzer:Schnirch|Schnirch]] 14:15, 14. Dez. 2010 (UTC)== | ||
| + | '''Voraussetzung:''' Zwei konvexe Punktmengen <math>\ M1 </math> und <math>\ M2 </math> mit <math>\ P \in M1 \cap M2 \and Q \in M1\cap M2 </math><br\> | ||
| + | '''Behauptung:''' <math> M1 \cap M2 </math> ist konvex, d. h. <math>\overline {PQ} \subseteq M1 \cap M2 </math> | ||
| + | |||
| + | {| class="wikitable " | ||
| + | |+ Beweis | ||
| + | ! Nr. | ||
| + | ! Beweisschritt | ||
| + | ! Begründung | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(I) | ||
| + | | <math>\ P \in M1 \and Q \in M1</math> | ||
| + | | <math>\ P </math> und <math>\ Q </math> sind nach Voraussetzung in der Schnittmenge <math>\ M1 \cap M2 </math>, also auch in <math>\ M1 </math> | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(II) | ||
| + | | <math>\ P \in M2 \and Q \in M2</math> | ||
| + | | <math>\ P </math> und <math>\ Q </math> sind nach Voraussetzung in der Schnittmenge <math>\ M1 \cap M2 </math>, also auch in <math>\ M2 </math> | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(III) | ||
| + | | <math>\overline{PQ}\subseteq M1 </math> | ||
| + | | (I) und der Voraussetzung, dass <math>\ M1 </math> konvex ist | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(IV) | ||
| + | | <math>\overline{PQ}\subseteq M2 </math> | ||
| + | | (II) und der Voraussetzung, dass <math>\ M2 </math> konvex ist | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(V) | ||
| + | | <math>\overline {PQ} \subseteq M1 \cap M2 </math> | ||
| + | | (III), (IV) und Definition Schnittmenge | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | ==vorausgegangene Lösungsvorschläge und Diskussionen== | ||
VSS: zwei konvexe Punktmengen o.B.d.A M1 und M2<br /> | VSS: zwei konvexe Punktmengen o.B.d.A M1 und M2<br /> | ||
Beh: Durchschnitt ist konvex<br /> | Beh: Durchschnitt ist konvex<br /> | ||
Beweisschritt Begründung<br /> | Beweisschritt Begründung<br /> | ||
| − | 1. A Element M1 geschnitten M2 und B Element Axiom vom Lineal<br /> | + | 1. A Element M1 geschnitten M2 und B Element Axiom vom Lineal<br /> |
M1 geschnitten M2<br /> | M1 geschnitten M2<br /> | ||
2. A,B sind Element von M1 und A,B Element M2 1<br /> | 2. A,B sind Element von M1 und A,B Element M2 1<br /> | ||
| Zeile 12: | Zeile 45: | ||
daraus folgt M1 geschnitten M2 ist konvex 4 | daraus folgt M1 geschnitten M2 ist konvex 4 | ||
--[[Benutzer:Sommer80|Sommer80]] 14:25, 30. Nov. 2010 (UTC) | --[[Benutzer:Sommer80|Sommer80]] 14:25, 30. Nov. 2010 (UTC) | ||
| + | zu 1. Die Begründung ist nicht korrekt, 1. folgt einfach aus der Voraussetzung, ansonsten OK!--[[Benutzer:Schnirch|Schnirch]] 14:15, 14. Dez. 2010 (UTC) | ||
| + | <u>2. Lösungsversuch:</u><br /> | ||
| + | <u>Vor</u>: M und N sind konvexe Punktmengen<br /> | ||
| + | <u>Beh:</u> Der Durchschnitt von M und N ist konvex<br /> | ||
| − | + | M ist konvex:<math>P \in M</math> und <math>Q \in M</math> daraus folgt <math>\overline{PQ}</math> ist Teilmenge von M<br /> | |
| − | + | N ist konvex:<math>P \in N</math> und <math>Q \in N</math> daraus folgt | |
| − | + | ||
| − | + | ||
| − | M ist konvex:<math>P \in | + | |
| − | N ist konvex:<math>P \in | + | |
<math>\overline{PQ}</math> ist Teilmenge von N<br /> | <math>\overline{PQ}</math> ist Teilmenge von N<br /> | ||
zu zeigen:<br /> | zu zeigen:<br /> | ||
| − | <math>P \in M\cap N </math> und <math>Q\in M\cap </math> daraus folgt <math>\overline{PQ}</math> ist Teilmenge<br /> | + | <math>P \in M\cap N </math> und <math>Q\in M\cap N</math> daraus folgt <math>\overline{PQ}</math> ist Teilmenge<br /> |
<math>\in M\cap N </math><br /> | <math>\in M\cap N </math><br /> | ||
| − | 1)<math>P \in M\cap N </math> und <math>Q\in M\cap </math> folgt aus<math>P \in N | + | 1)<math>P \in M\cap N </math> und <math>Q\in M\cap N </math> folgt aus<math>P \in N</math> und <math>P \in N</math> daraus folgt <math>\overline{PQ}</math><br /> Teilmenge von N |
| − | 2)<math>P \in M\cap N </math> und <math>Q\in M\cap N </math> folgt aus <math>P \in | + | 2)<math>P \in M\cap N </math> und <math>Q\in M\cap N </math> folgt aus <math>P \in M</math> und <math>P \in M</math> daraus folgt<math>\overline{PQ}</math><br /> Teilmenge von M |
| − | 3) 1) und 2) Aus <math>\overline{PQ}</math> Teilmenge von M und<math>\overline{PQ}</math> Teilmenge von N folgt nach Def. einer konvexen Punktmenge | + | 3) 1) und 2) Aus <math>\overline{PQ}</math> Teilmenge von M und<math>\overline{PQ}</math> Teilmenge von N folgt nach Def. einer konvexen Punktmenge <math>P \in M\cap N </math> und <math>Q\in M\cap N </math><br />--[[Benutzer:Engel82|Engel82]] 19:53, 30. Nov. 2010 (UTC) |
| + | die Lösung von Engel82 ist auch OK!--[[Benutzer:Schnirch|Schnirch]] 14:15, 14. Dez. 2010 (UTC) | ||
| + | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 14. Dezember 2010, 15:16 Uhr
Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex.
Lösung --Schnirch 14:15, 14. Dez. 2010 (UTC)
Voraussetzung: Zwei konvexe Punktmengen 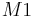 und
und 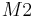 mit
mit 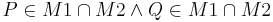
Behauptung: 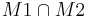 ist konvex, d. h.
ist konvex, d. h. 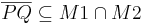
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 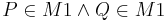
|
 und und  sind nach Voraussetzung in der Schnittmenge sind nach Voraussetzung in der Schnittmenge 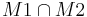 , also auch in , also auch in 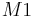
|
| (II) | 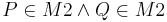
|
 und und  sind nach Voraussetzung in der Schnittmenge sind nach Voraussetzung in der Schnittmenge 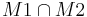 , also auch in , also auch in 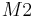
|
| (III) | 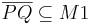
|
(I) und der Voraussetzung, dass 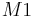 konvex ist konvex ist
|
| (IV) | 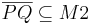
|
(II) und der Voraussetzung, dass 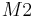 konvex ist konvex ist
|
| (V) | 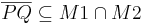
|
(III), (IV) und Definition Schnittmenge |
vorausgegangene Lösungsvorschläge und Diskussionen
VSS: zwei konvexe Punktmengen o.B.d.A M1 und M2
Beh: Durchschnitt ist konvex
Beweisschritt Begründung
1. A Element M1 geschnitten M2 und B Element Axiom vom Lineal
M1 geschnitten M2
2. A,B sind Element von M1 und A,B Element M2 1
3. Strecke AB ist Element von M1 VSS, 1, Definition konvex
4. Strecke AB ist Element von M2 VSS, 1, Definition konvex
5. Strecke AB ist Teilmenge von M1 und M2,
daraus folgt M1 geschnitten M2 ist konvex 4
--Sommer80 14:25, 30. Nov. 2010 (UTC)
zu 1. Die Begründung ist nicht korrekt, 1. folgt einfach aus der Voraussetzung, ansonsten OK!--Schnirch 14:15, 14. Dez. 2010 (UTC)
2. Lösungsversuch:
Vor: M und N sind konvexe Punktmengen
Beh: Der Durchschnitt von M und N ist konvex
M ist konvex: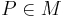 und
und 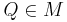 daraus folgt
daraus folgt  ist Teilmenge von M
ist Teilmenge von M
N ist konvex: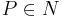 und
und 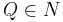 daraus folgt
daraus folgt
 ist Teilmenge von N
ist Teilmenge von N
zu zeigen:
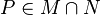 und
und 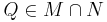 daraus folgt
daraus folgt  ist Teilmenge
ist Teilmenge
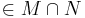
1)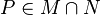 und
und 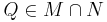 folgt aus
folgt aus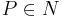 und
und 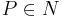 daraus folgt
daraus folgt 
Teilmenge von N
2)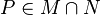 und
und 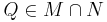 folgt aus
folgt aus 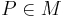 und
und 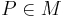 daraus folgt
daraus folgt
Teilmenge von M
3) 1) und 2) Aus  Teilmenge von M und
Teilmenge von M und Teilmenge von N folgt nach Def. einer konvexen Punktmenge
Teilmenge von N folgt nach Def. einer konvexen Punktmenge 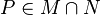 und
und 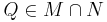
--Engel82 19:53, 30. Nov. 2010 (UTC)
die Lösung von Engel82 ist auch OK!--Schnirch 14:15, 14. Dez. 2010 (UTC)

