Lösung von Aufg. 10.2: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
Eine Gerade g und eine Ebene <math>\epsilon</math> stehen senkrecht aufeinander, wenn es in <math>\epsilon</math> zwei Geraden gibt, die sich schneiden und jeweils senkrecht zu g stehen.<br />--[[Benutzer:Engel82|Engel82]] 15:49, 15. Dez. 2010 (UTC)<br /> | Eine Gerade g und eine Ebene <math>\epsilon</math> stehen senkrecht aufeinander, wenn es in <math>\epsilon</math> zwei Geraden gibt, die sich schneiden und jeweils senkrecht zu g stehen.<br />--[[Benutzer:Engel82|Engel82]] 15:49, 15. Dez. 2010 (UTC)<br /> | ||
| − | diese Definition von Engel82 ist korrekt! | + | diese Definition von Engel82 ist korrekt!--[[Benutzer:Schnirch|Schnirch]] 15:19, 19. Jan. 2011 (UTC) |
... wenn es in <math>\epsilon</math> zwei voneinander verschiedene Geraden gibt, die senkrecht zu g stehen. --[[Benutzer:Jp1234|jp1234]] 23:35, 21. Dez. 2010 (UTC)<br /> | ... wenn es in <math>\epsilon</math> zwei voneinander verschiedene Geraden gibt, die senkrecht zu g stehen. --[[Benutzer:Jp1234|jp1234]] 23:35, 21. Dez. 2010 (UTC)<br /> | ||
| − | wenn die beiden Geraden ''f'' und ''h'' in der Ebene parallel zueinander stehen, dann gebe es eine dritte Gerade ''g'' in der Ebene, die senkrecht auf die beiden Geraden ''f'' und ''h'' stehen würde und nach Ihrer Definition damit senkrecht auf der Ebene stünde. Da unsere Gerade ''g'' aber in der Ebene liegt, stimmt dies offensichtlich nicht!--[[Benutzer:Schnirch|Schnirch]] 15:16, 19. Jan. 2011 (UTC) | + | wenn die beiden Geraden ''f'' und ''h'' in der Ebene parallel zueinander stehen, dann gebe es eine dritte Gerade ''g'' in der Ebene,<br />die senkrecht auf die beiden Geraden ''f'' und ''h'' stehen würde und nach Ihrer Definition damit senkrecht auf der Ebene stünde.<br />Da unsere Gerade ''g'' aber in der Ebene liegt, stimmt dies offensichtlich nicht!--[[Benutzer:Schnirch|Schnirch]] 15:16, 19. Jan. 2011 (UTC) |
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 19. Januar 2011, 16:19 Uhr
Definition V.9 : (noch mehr Senkrecht)
- Eine Gerade
und eine Strecke 
stehen senkrecht aufeinander, wenn die und die Gerade 
senkrecht aufeinander stehen.
- Eine Gerade
Ergänzen Sie:
- Eine Strecke
und eine Strecke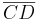 
stehen senkrecht aufeinander, wenn ... .
- Eine Strecke
- Eine Gerade und eine Ebene
stehen senkrecht aueinander, wenn es in ... .
- Eine Gerade
Eine Strecke und eine Strecke 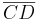stehen senkrecht aufeinander, wenn auch die Geraden und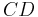 
senkrecht aufeinander stehen.
die Def. ist korrekt, das Wörtchen "auch" können Sie allerdings weglassen.--Schnirch 15:16, 19. Jan. 2011 (UTC)
Eine Gerade g und eine Ebene stehen senkrecht aufeinander, wenn es in zwei Geraden gibt, die sich schneiden und jeweils senkrecht zu g stehen.
--Engel82 15:49, 15. Dez. 2010 (UTC)
diese Definition von Engel82 ist korrekt!--Schnirch 15:19, 19. Jan. 2011 (UTC)
... wenn es in zwei voneinander verschiedene Geraden gibt, die senkrecht zu g stehen. --jp1234 23:35, 21. Dez. 2010 (UTC)
wenn die beiden Geraden f und h in der Ebene parallel zueinander stehen, dann gebe es eine dritte Gerade g in der Ebene,
die senkrecht auf die beiden Geraden f und h stehen würde und nach Ihrer Definition damit senkrecht auf der Ebene stünde.
Da unsere Gerade g aber in der Ebene liegt, stimmt dies offensichtlich nicht!--Schnirch 15:16, 19. Jan. 2011 (UTC)
