Lösung von Aufg. 12.6: Unterschied zwischen den Versionen
| (7 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
1) Es existiert genau eine Gerade h für die gilt:___________________________WInkelkonstruktionsaxiom<br /> | 1) Es existiert genau eine Gerade h für die gilt:___________________________WInkelkonstruktionsaxiom<br /> | ||
<math>\alpha1 </math> <math>\cong</math><math>\beta </math><br /> | <math>\alpha1 </math> <math>\cong</math><math>\beta </math><br /> | ||
| − | 2)h//b________________________Umkehrung des Stufenwinkelsatzes<br /> | + | 2) h//b________________________Umkehrung des Stufenwinkelsatzes und 1) <br /> |
| − | 3) Die Gerade b hat zwei Parallelen a und | + | 3) Die Gerade b hat zwei Parallelen a und h______________________ Vor. und 2) Widerspruch zum EPA<br /> |
| − | 4) a= | + | 4) a=h___________________________3)<br /> |
5) Annahme ist zu verwerfen<br /> | 5) Annahme ist zu verwerfen<br /> | ||
6) Behauptung stimmt --[[Benutzer:Engel82|Engel82]] 17:57, 19. Jan. 2011 (UTC)<br /> | 6) Behauptung stimmt --[[Benutzer:Engel82|Engel82]] 17:57, 19. Jan. 2011 (UTC)<br /> | ||
| Zeile 17: | Zeile 17: | ||
| − | + | Musst du für diesen Beweis nicht erstmal die Umkehrung des Stufenwinkelsatz beweisen...das haben wir ja noch nicht gemacht?!<br /> | |
| + | doch haben wir, erinnern Sie sich, die Umkehrung des Stufenwinkelsatzes gehört in<br /> die Absolute, der Stufenwinkelsatz selbst aber in die Euklidische Geometrie!<br /> Der Beweis ist korrekt!--[[Benutzer:Schnirch|Schnirch]] 10:51, 4. Feb. 2011 (UTC) | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
| + | |||
| + | Andere Möglichkeit, könnte das gehen? | ||
| + | |||
| + | Vor.: aIIb | ||
| + | |||
| + | Beh.: IαI = IβI | ||
| + | |||
| + | 1) aIIb_____________________________Vor. | ||
| + | |||
| + | 2) IαI+IάI=180_______________________1), Supplementaxiom, Definition Nebenwinkel | ||
| + | |||
| + | 3) IάI=Iβ’I___________________________Stufenwinkelsatz | ||
| + | |||
| + | 4) IβI+Iβ’I=180_______________________1), Supplementaxiom, Definition Nebenwinkel | ||
| + | |||
| + | 5) IαI+I β’I=180______________________2),3),4) | ||
| + | |||
| + | 6) IαI=IβI___________________________5) | ||
| + | |||
| + | 7) Behauptung stimmt<br /><br /> | ||
| + | |||
| + | Du benutzt in deinem Beweis zum Stufenwinkelsatz ja bereits den Stufenwinkelsatz...<br /> | ||
| + | richtig, das wäre ein typischer Zirkelschluss und nicht erlaubt!--[[Benutzer:Schnirch|Schnirch]] 10:51, 4. Feb. 2011 (UTC) | ||
| + | |||
| + | Ich würde das so machen:<br /> | ||
| + | Vor.: a||b und c schneidet a und b<br /> | ||
| + | Beh.: <math> |\alpha| </math> = <math> |\alpha_1| </math> <br /> | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1) <math> a \cap c = {S}</math> und <math> c \cap b = {B}</math> || Vor. | ||
| + | |- | ||
| + | | 2) <math> \overline {SL_b} </math> Lot von S auf b|| Definition Lot, 1) | ||
| + | |- | ||
| + | | 3) <math> \exists L_d </math> <math>\in SL_b^- </math> : <math> \overline {|SL_d|} </math> = <math> \overline {|SL_d|} </math> || Axiom vom Lineal, 2) | ||
| + | |- | ||
| + | | 4) <math> \exists d </math> : <math> d \|a </math> und <math> L_d </math> <math>\in d </math> und <math> d \cap c = {D}</math> || Euklidisches Parallelenaxiom, 3) | ||
| + | |- | ||
| + | | 5) <math> \overline {SL_d} </math> Lot von S auf d || Definition Lot, 4) | ||
| + | |- | ||
| + | | 6) <math> \angle BL_bS </math> <math> \cong </math> <math> \angle DL_dS </math> || 2), 5) | ||
| + | |- | ||
| + | | 7) <math> \angle L_bSB </math> <math> \cong </math> <math> \angle L_dSD </math> || Scheitelwinkelsatz, 1) | ||
| + | |- | ||
| + | | 8) <math> \overline {BL_bS} </math> <math> \cong </math> <math> \overline {DL_dS} </math>|| 3),6),7), SWS-Axiom | ||
| + | |- | ||
| + | | 9) <math> \angle SBL_b </math> <math> \cong </math> <math> \angle SDL_d </math> || 8), Definition Dreieckskongruenz | ||
| + | |- | ||
| + | | 10) <math> \angle \alpha_2 </math> <math> \cong </math> <math> \angle \alpha_1 </math> || 9), Wechselwinkelsatz | ||
| + | |- | ||
| + | | 11) <math> \angle \alpha_1 </math> <math> \cong </math> <math> \angle \alpha </math> || 9),10) | ||
| + | |} | ||
| + | --[[Benutzer:Jbo-sax|Jbo-sax]] 20:22, 25. Jan. 2011 (UTC)<br /> | ||
| + | |||
| + | Sie haben in Schritt 3 ein Lot konstruiert auf eine Gerade d, die Sie aber erst anschließend<br /> in Schritt 4 erzeugen, dass ist etwas seltsam?--[[Benutzer:Schnirch|Schnirch]] 10:51, 4. Feb. 2011 (UTC) | ||
Aktuelle Version vom 4. Februar 2011, 11:51 Uhr
Aufgabe 12.6
Beweisen Sie den Stufenwinkelsatz.
Vor: a//b
Beh: 


Annahme:  ist nicht kongruent zu
ist nicht kongruent zu 
1) Es existiert genau eine Gerade h für die gilt:___________________________WInkelkonstruktionsaxiom
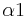


2) h//b________________________Umkehrung des Stufenwinkelsatzes und 1)
3) Die Gerade b hat zwei Parallelen a und h______________________ Vor. und 2) Widerspruch zum EPA
4) a=h___________________________3)
5) Annahme ist zu verwerfen
6) Behauptung stimmt --Engel82 17:57, 19. Jan. 2011 (UTC)
Musst du für diesen Beweis nicht erstmal die Umkehrung des Stufenwinkelsatz beweisen...das haben wir ja noch nicht gemacht?!
doch haben wir, erinnern Sie sich, die Umkehrung des Stufenwinkelsatzes gehört in
die Absolute, der Stufenwinkelsatz selbst aber in die Euklidische Geometrie!
Der Beweis ist korrekt!--Schnirch 10:51, 4. Feb. 2011 (UTC)
Andere Möglichkeit, könnte das gehen?
Vor.: aIIb
Beh.: IαI = IβI
1) aIIb_____________________________Vor.
2) IαI+IάI=180_______________________1), Supplementaxiom, Definition Nebenwinkel
3) IάI=Iβ’I___________________________Stufenwinkelsatz
4) IβI+Iβ’I=180_______________________1), Supplementaxiom, Definition Nebenwinkel
5) IαI+I β’I=180______________________2),3),4)
6) IαI=IβI___________________________5)
7) Behauptung stimmt
Du benutzt in deinem Beweis zum Stufenwinkelsatz ja bereits den Stufenwinkelsatz...
richtig, das wäre ein typischer Zirkelschluss und nicht erlaubt!--Schnirch 10:51, 4. Feb. 2011 (UTC)
Ich würde das so machen:
Vor.: a||b und c schneidet a und b
Beh.: 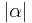 =
= 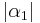
1) 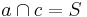 und und 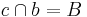 |
Vor. |
2) 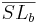 Lot von S auf b Lot von S auf b |
Definition Lot, 1) |
3) 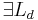 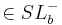 : : 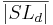 = = 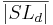 |
Axiom vom Lineal, 2) |
4) 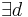 : : 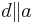 und und 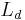 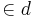 und und 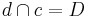 |
Euklidisches Parallelenaxiom, 3) |
5) 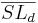 Lot von S auf d Lot von S auf d |
Definition Lot, 4) |
6) 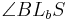  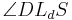 |
2), 5) |
7) 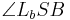  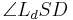 |
Scheitelwinkelsatz, 1) |
8) 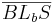  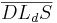 |
3),6),7), SWS-Axiom |
9) 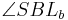  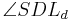 |
8), Definition Dreieckskongruenz |
10) 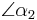  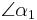 |
9), Wechselwinkelsatz |
11) 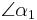  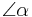 |
9),10) |
--Jbo-sax 20:22, 25. Jan. 2011 (UTC)
Sie haben in Schritt 3 ein Lot konstruiert auf eine Gerade d, die Sie aber erst anschließend
in Schritt 4 erzeugen, dass ist etwas seltsam?--Schnirch 10:51, 4. Feb. 2011 (UTC)

