Lösung von Aufg. 13.4: Unterschied zwischen den Versionen
| (7 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
Erläutern Sie wie und beweisen Sie dass die Schüler von Frau Schultze-Kröttendörfer durch die genannten Faltungen aus den Parallelogrammen Rauten generieren. | Erläutern Sie wie und beweisen Sie dass die Schüler von Frau Schultze-Kröttendörfer durch die genannten Faltungen aus den Parallelogrammen Rauten generieren. | ||
| − | Vor: AF+ und DF+ sind Winkelhalbierende | + | <u>Vor</u>: AF+ und DF+ sind Winkelhalbierende der Winkel <math>\angle BAD</math> und <math>\angle ADC</math> |
| − | Beh: <math>\overline {AD}</math><math>\cong</math> <math>\overline {DE}</math><math>\overline {EF}</math><math>\cong</math> <math>\overline {AF}</math> | + | <br /> |
| + | |||
| + | <u>Beh:</u> <math>\overline {AD}</math><math>\cong</math> <math>\overline {DE}</math><math>\cong</math> <math>\overline {EF}</math><math>\cong</math> <math>\overline {AF}</math> | ||
| + | |||
| + | 1)<math>\angle FAE</math> <math>\cong</math><math>\angle EAD</math>__________________AE+ ist Winkelhalbierende des <math>\angle BAD</math> und<br /> | ||
| + | <math>\angle EDF</math><math>\cong</math><math>\angle ADF</math>__________________DF+ ist Winkelhalbierende des <math>\angle ADC</math><br /> | ||
| + | |||
| + | 2)<math>\angle FAE</math><math>\cong</math><math>\angle AED</math> und______________Wechselwinkel an geschnittenen Parallelen<br /> | ||
| + | <math>\angle EDF</math><math>\cong</math><math>\angle AFD</math><br /> | ||
| + | |||
| + | 3)<math>\angle EAD</math> <math>\cong</math><math>\angle AED</math>__________________1),2) und Transitivität der Winkelkongruenz<br /> | ||
| + | |||
| + | 4)<math>\overline {AD}</math><math>\cong</math> <math>\overline {DE}</math>______3) und Umkehrung des Basiswinkelsatzes<br /> | ||
| + | |||
| + | 5)<math>\angle AFD</math> <math>\cong</math><math>\angle ADF</math>_____________1),2) und Transitivität der Winkelkongruenz <br /> | ||
| + | |||
| + | 6)<math>\overline {AD}</math><math>\cong</math> <math>\overline {AF}</math>_____5) und Umkehrung des Basiswinkelsatzes<br /> | ||
| + | |||
| + | 7)<math>\triangle {ADP}</math> <math>\cong</math><math>\triangle {DPE}</math>_______WSW,1),3),4)<br /> | ||
| + | |||
| + | |||
| + | analoge Beweisführung für das <math>\triangle {AEF}</math><br /> | ||
| + | daraus folgt letzendlich die Behauptung <math>\overline {AD}</math><math>\cong</math> <math>\overline {DE}</math><math>\cong</math> <math>\overline {EF}</math><math>\cong</math> <math>\overline {AF}</math>--[[Benutzer:Engel82|Engel82]]11:45, 26. Jan. 2011 (UTC)<br /><br /> | ||
| + | |||
| + | Wow, da muss man ja schon beim Nachvollziehen schauen, dass man den richtigen Winkel erwischt, wie muss das erst beim Aufschreiben gewesen sein?! Hut ab.--[[Benutzer:Jbo-sax|Jbo-sax]] 14:08, 29. Jan. 2011 (UTC)<br /><br /> | ||
| + | |||
| + | Was ist der Punkt P? Das sollten Sie noch klären (Schnittpunkt der beiden Winkelhalbierenden),<br />bevor Sie den Punkt verwenden, ansonsten ist der Beweis korrekt!<br />Tipp: Machen Sie sich in der Klausur immer eine Zeichnung und bezeichnen Sie die Winkel<br /> schulüblich mit <math>\alpha</math>,<math>\beta</math>, <math>\gamma</math> usw.<br /> - das erleichtert Ihnen die Arbeit.--[[Benutzer:Schnirch|Schnirch]] 14:00, 4. Feb. 2011 (UTC)<br /> | ||
| + | |||
Aktuelle Version vom 4. Februar 2011, 15:00 Uhr
Frau Schultze-Kröttendörfer räumt ihren Schrank auf. Es findet sich ein Stapel Arbeitsblätter, auf die ein Parallelogramm gedruckt wurde, welches keine Raute ist. "Zu dumm", denkt Frau Schultze-Kröttendörfer, "ich brauche Arbeitsblätter mit Rauten". Kurz darauf kommt ihr eine zündende Idee. Sie wird den Begriff der Raute konstruktiv erarbeiten lassen. Diesbezüglich wird sie den Schülern den Auftrag geben, die Parallelogramme auf den vorhandenen Arbeitsblättern auszuschneiden und dann so zu falten, dass zwei benachbarte Seiten des Parallelogramms zur Deckung kommen. Erläutern Sie wie und beweisen Sie dass die Schüler von Frau Schultze-Kröttendörfer durch die genannten Faltungen aus den Parallelogrammen Rauten generieren.
Vor: AF+ und DF+ sind Winkelhalbierende der Winkel 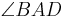 und
und 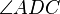
Beh: 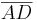

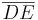

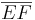

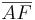
1)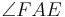

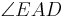 __________________AE+ ist Winkelhalbierende des
__________________AE+ ist Winkelhalbierende des 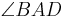 und
und
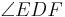

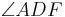 __________________DF+ ist Winkelhalbierende des
__________________DF+ ist Winkelhalbierende des 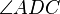
2)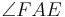

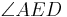 und______________Wechselwinkel an geschnittenen Parallelen
und______________Wechselwinkel an geschnittenen Parallelen
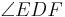

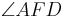
3)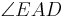

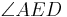 __________________1),2) und Transitivität der Winkelkongruenz
__________________1),2) und Transitivität der Winkelkongruenz
4)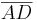

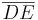 ______3) und Umkehrung des Basiswinkelsatzes
______3) und Umkehrung des Basiswinkelsatzes
5)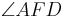

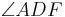 _____________1),2) und Transitivität der Winkelkongruenz
_____________1),2) und Transitivität der Winkelkongruenz
6)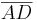

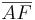 _____5) und Umkehrung des Basiswinkelsatzes
_____5) und Umkehrung des Basiswinkelsatzes
7)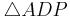

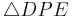 _______WSW,1),3),4)
_______WSW,1),3),4)
analoge Beweisführung für das 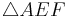
daraus folgt letzendlich die Behauptung 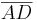

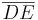

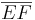

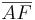 --Engel8211:45, 26. Jan. 2011 (UTC)
--Engel8211:45, 26. Jan. 2011 (UTC)
Wow, da muss man ja schon beim Nachvollziehen schauen, dass man den richtigen Winkel erwischt, wie muss das erst beim Aufschreiben gewesen sein?! Hut ab.--Jbo-sax 14:08, 29. Jan. 2011 (UTC)
Was ist der Punkt P? Das sollten Sie noch klären (Schnittpunkt der beiden Winkelhalbierenden),
bevor Sie den Punkt verwenden, ansonsten ist der Beweis korrekt!
Tipp: Machen Sie sich in der Klausur immer eine Zeichnung und bezeichnen Sie die Winkel
schulüblich mit,
,
usw.
- das erleichtert Ihnen die Arbeit.--Schnirch 14:00, 4. Feb. 2011 (UTC)

