Definition der Woche 7 (SoSe 11): Unterschied zwischen den Versionen
HecklF (Diskussion | Beiträge) |
|||
| (11 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Definieren Sie den Begriff "Halbkreis". | Definieren Sie den Begriff "Halbkreis". | ||
<br /> | <br /> | ||
| − | Sei k ein Kreis (bzw. die Menge aller Punkte, die von einem Punkt M ein und den selben Abstand haben) und Strecke d eine Kreissehne für die gilt: Mittelpunkt M | + | Sei k ein Kreis (bzw. die Menge aller Punkte, die von einem Punkt M ein und den selben Abstand haben) und Strecke d eine Kreissehne für die gilt: Mittelpunkt M <math>\in</math> d. <br /> |
Die Menge aller Punkte, die von M ein und den selben Abstand haben und Unterhalb der Sehne d liegen, heißt Halbkreis. <br /> | Die Menge aller Punkte, die von M ein und den selben Abstand haben und Unterhalb der Sehne d liegen, heißt Halbkreis. <br /> | ||
| Zeile 7: | Zeile 7: | ||
| + | Definition Halbkreis:<br /> | ||
| + | Sei k ein Kreis (s.o) mit dem Mittelpunk M und dem Durchmesser d.<br /> | ||
| + | Sei X <math>\in</math> k und X <math>\not\in</math> von d.<br /> | ||
| + | H := {y <math>\in</math> k | <math>\overline {XY}</math> geschnitten d ={} }<br /> | ||
| + | H heißt Halbkreis.<br /> | ||
| + | Je nach Wahl von X ergeben sich zwei verschiedene Halbkreise<br />--[[Benutzer:Peterpummel|Peterpummel]] 20:23, 17. Mai 2011 (CEST)<br /> | ||
| + | Hallo Peterpummel,<br \> | ||
| + | das musst du bitte kurz erklären. ich hab das was du beschrieben hast mal nach bestem Wissen und Gewissen im Geogebra generiert und siehe da - alles andere als ein Halbkreis. <br /> | ||
| + | <br /> | ||
| + | |||
| + | [[Bild:halbkreis.jpg]] | ||
| + | |||
| + | <br /> | ||
| + | ich denke um einen Halbkreis zu generieren, ist es entscheident, im Zentrum des Kreises, also im Mittelpunkt anzufangen, wenn du auf dem Kreis, aus dem dein Halbkreis entstehen soll, einen Punkt legst und daran arbeitest gehst du fehl. | ||
| + | |||
| + | <br /> | ||
| + | sollte ich mich jedoch wahnsinnig geirrt haben, dann gerne eine Verbesserung. --[[Benutzer:HecklF|Flo60]] 22:57, 17. Mai 2011 (CEST) | ||
| + | <br /> | ||
| + | |||
| + | '''STOP: Ich nehme alles zurück und behaupte das Gegenteil :-) was ich unterschlagen habe war das Y <math>\in</math> k ist, dann macht es Sinn. | ||
| + | |||
| + | Ich lasse aber die Graphik trotzdem drinn, dann können ein paar andere evtl. noch ein wenig knobeln.''' | ||
[[Kategorie:Einführung_Geometrie]] | [[Kategorie:Einführung_Geometrie]] | ||
| + | |||
| + | Huhu Flo60,<br /> | ||
| + | eine Frage zu deiner Zeichnung, müsste der rote Kreis nicht noch "etwas" näher an d ? :) --[[Benutzer:Peterpummel|Peterpummel]] 19:16, 18. Mai 2011 (CEST) | ||
| + | |||
| + | Vielleicht hilft das:--[[Benutzer:*m.g.*|*m.g.*]] 18:39, 23. Mai 2011 (CEST)<br /> | ||
| + | <ggb_applet width="535" height="528" version="3.2" ggbBase64="UEsDBBQACAAIAJWTtz4AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5Vjfb+M2DH7e/RWCH4btIYllO46DJT2kPWArcNcO6O3Q7k22mUSrf02W26R//SjJTpyk7ZI2t+thT7IpmiI/fqRpj94v0oTcgSh5no0t2rUtAlmUxzybja1KTjuB9f7k3WgG+QxCwcg0FymTY8vtOpaSV/zk3Q+jcp7fE5ZolS8c7sfWlCUlWKQsBLC4nAPIDTmrFjzhTCwvw78gkuV6wxg5z4oKT5GiQlmUxh952dz29IFFwuUHfsdjECTJo7Hl99F1vPoCQvKIJWPLs43EGVvO1iaKXLU7zwV/yDOp1NfGpyghpOQPgE96Sjbq6UBHUEUJjznLVDDaD1Qi5J7Hcj62+m4fTQKfzdFXbxAYa1Gei/hqWUpIyeJPEDkaHTgK6GV957rqrkS/8MC+rbfad9oM3F2BlJiWkrAFrAGbCR5v3JyXp3myFhU5z+QZK2QldE7dWnQll+oAPEsohyfZLIFa5iDkc4huw3xxpUGgrjH9eVnoR7RD4ewsT3JBhIIXA5/Va2hWraM8XWnZWsfWGrUNZXS1T4eO1tBraFatlfDMuFZHTpuoqd0cw0uiBApGpOIq+ISFgKm1SJVx+bG5QQrc1qFS88BFlYZYA20SrGzSY9kc9bboM7oFkUFiSJJhbqu8KsmdIqM5SzsSQ8RTvDUbNSRMpesPdMBIY5gJaBw3FWQA07t2m4hb4lGvcUL5UKKvkcRWgPFIFcsHmHI8RUl+Y0l4K4CXqnolVs7Y+pWDahQWiZlEZdUQIIEUsHykpopm2gqyT9aqV+S67JsCr/fX4OP2o7TRBGNJMWcoaSojYUtsAu1Itb1PebwZP8sQRx0K1mKhDKhMFQAmybImNynQoC6VVhI0diVZmGPJsl4fTMvUKqaqVD/Qh7p1yg0eO8hkVQqCR6vYhcYGn6zq573G7gZemxxsOfgUYnYLL7onXvS1eLXDjvI0ZVlMMpai+hkXUQI6Vq5aPGG24gVhVEFgIqlksxEZY7WJHQyRsC0EI2uzV8g5lmQGZakbmmy3ruNBeiAF9/IOXyCQ3aFvuSgJWdj1a3lpN6RrJAsErWP4SGvRA20xErMn+IJMGv1JozXB91+H+vrSra1OvMbYpF9fGW/+zozHpeluSICIT3n0fJ7PM4m9D2PYSnVkUr2YYHfdSffEbJ4+n/XNnjJ5UU/xPZ1PtYRm2TOjl9NpCVL1gQ4dmj7wXL7XbaPjHadvbEZ/+t9G/0x8TXidg+PbJM4VzJR8izZtZmxQhj3PlbK21uDBXtgjNkD9ui1i900T1IiuTe3VRbbqlqc4MkdcriBMVNNe1Sm2+d3R4xagUDPfZfZZsKxUs7/RaY00T+Txd83T7eLfTt/1IaV+/SKyU8fMpnp97Qgx5QuINyFoZ8zpDnzXc6kd+DTo40eHoxPodIMhHfrOwPd86ngD2n9NheyH7M0hyN58e2SPM5x13K5v+4HvBEHfDoaObfs6A7Q7cIYuHQQOxcxQanvH71E3pkdd76QiPKxHhd9Tj+rQLvUd3/OGnjMceq5PNd5+1x3YiPhwQJ2B5/WphrtD+13HHmKNDAI/QG2n//00tCtI8bRHptdTk/fJTt7jPabXgol15uOnMz98SebxhNh8uyn1y2beJT8m8heySnqbH82H/NcZdLeDeNuD7lvh15OzDxzKL3iaX4Oj8mv2bfi1HcT/nF+wKATiovLT5M4iKBxby59ufrZI719/Sky3f0o88h497O/D4V+MzNA/3KH/2SETztmb+VC6YBf6FanXB7PuNYP02v/n9C/p+p/8yT9QSwcIogTLMTwFAADFFwAAUEsBAhQAFAAIAAgAlZO3PqIEyzE8BQAAxRcAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAB2BQAAAAA=" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "true" allowRescaling = "true" /><br /><br /> | ||
| + | Bewegen Sie mit der Maus den Punkt <math>\ Y</math>. | ||
| + | <br /><br/> | ||
| + | ich kann das ganze nicht anschauen, obgleich ich (für geogebra obligatorisch) java bereits auf meinem rechner installiert habe. | ||
| + | vielleicht kann man einen screenshot oder einen dateidownload anhängen - wäre zwar sicherlich aufwendig aber fänd ich superklasse. dankeschön --[[Benutzer:HecklF|Flo60]] 14:32, 25. Mai 2011 (CEST)<br /><br /> | ||
| + | <br /> | ||
| + | '''Ist diese Definition korrekt?''' <br /> Definition : Halbkreis:<br /> | ||
| + | Es sei k ein Kreis mit dem Durchmesser <math>\overline{AB}</math> . Ferner sei X ein belibiger Punkt auf k mit <math>A\neq X, B\neq X</math>. Die Menge aller Punkte Y für die gilt: <math>\overline{XY} \ \cap AB =\lbrace \rbrace</math> heißt Halbkreis von Kreis k. | ||
| + | <br />--[[Benutzer:Herbst2010|Herbst2010]] 11:14, 5. Jul. 2011 (CEST) | ||
Aktuelle Version vom 5. Juli 2011, 10:14 Uhr
Definieren Sie den Begriff "Halbkreis".
Sei k ein Kreis (bzw. die Menge aller Punkte, die von einem Punkt M ein und den selben Abstand haben) und Strecke d eine Kreissehne für die gilt: Mittelpunkt M 
d.
Die Menge aller Punkte, die von M ein und den selben Abstand haben und Unterhalb der Sehne d liegen, heißt Halbkreis.
Man könnte jetzt natürlich annehmen: "Was ist mit den ganzen Punkten, die Oberhalb der Sehen liegen." Aber aufgrund der Invarianz denke ich dass es soweit keine Rolle spielt.
Definition Halbkreis:
Sei k ein Kreis (s.o) mit dem Mittelpunk M und dem Durchmesser d.
Sei X k und X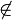 
von d.
H := {y k |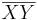 
geschnitten d ={} }
H heißt Halbkreis.
Je nach Wahl von X ergeben sich zwei verschiedene Halbkreise
--Peterpummel 20:23, 17. Mai 2011 (CEST)
Hallo Peterpummel,
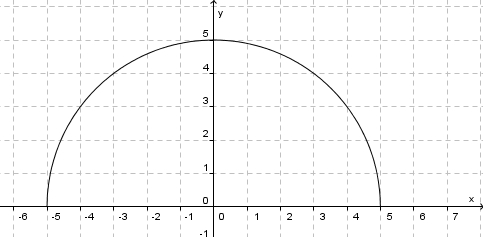
das musst du bitte kurz erklären. ich hab das was du beschrieben hast mal nach bestem Wissen und Gewissen im Geogebra generiert und siehe da - alles andere als ein Halbkreis.
ich denke um einen Halbkreis zu generieren, ist es entscheident, im Zentrum des Kreises, also im Mittelpunkt anzufangen, wenn du auf dem Kreis, aus dem dein Halbkreis entstehen soll, einen Punkt legst und daran arbeitest gehst du fehl.
sollte ich mich jedoch wahnsinnig geirrt haben, dann gerne eine Verbesserung. --Flo60 22:57, 17. Mai 2011 (CEST)
STOP: Ich nehme alles zurück und behaupte das Gegenteil :-) was ich unterschlagen habe war das Y k ist, dann macht es Sinn.
Ich lasse aber die Graphik trotzdem drinn, dann können ein paar andere evtl. noch ein wenig knobeln.
Huhu Flo60,
eine Frage zu deiner Zeichnung, müsste der rote Kreis nicht noch "etwas" näher an d ? :) --Peterpummel 19:16, 18. Mai 2011 (CEST)
Vielleicht hilft das:--*m.g.* 18:39, 23. Mai 2011 (CEST)
Bewegen Sie mit der Maus den Punkt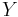 
.
ich kann das ganze nicht anschauen, obgleich ich (für geogebra obligatorisch) java bereits auf meinem rechner installiert habe.
vielleicht kann man einen screenshot oder einen dateidownload anhängen - wäre zwar sicherlich aufwendig aber fänd ich superklasse. dankeschön --Flo60 14:32, 25. Mai 2011 (CEST)
Ist diese Definition korrekt?
Definition : Halbkreis:
Es sei k ein Kreis mit dem Durchmesser 
. Ferner sei X ein belibiger Punkt auf k mit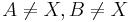 
. Die Menge aller Punkte Y für die gilt: 
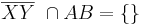heißt Halbkreis von Kreis k.
--Herbst2010 11:14, 5. Jul. 2011 (CEST)
