Probeklausur (SoSe 11): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→d) |
(→1. b) |
||
| (9 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | ==Bemerkungen vorab== | ||
| + | Die Probeklausuren sind geschrieben. Das Bild, das sich dabei bei einigen Kommilitonen bot, ist erschreckend. Wer nach der Intensität, mit der wir auf den Begriffen ''Strecke'' oder ''Inneres eines Winkels'' herumgeritten sind, nicht ad hoc auch ohne explizite Vorbereitung eine entsprechende Definition anbieten kann, hat definitiv nicht verstanden, wie und in welcher Form Mathematik gelernt werden muss.--[[Benutzer:*m.g.*|*m.g.*]] 18:47, 26. Jun. 2011 (CEST) | ||
==Die Klausur als PDF== | ==Die Klausur als PDF== | ||
{{pdf|Probeklausur_SS_11.pdf|Probeklausur_SS_11}} | {{pdf|Probeklausur_SS_11.pdf|Probeklausur_SS_11}} | ||
| Zeile 13: | Zeile 15: | ||
<math>M</math>'' versteht. | <math>M</math>'' versteht. | ||
| − | |||
[[Lösung_Aufgabe_1b_SS11]] | [[Lösung_Aufgabe_1b_SS11]] | ||
| Zeile 29: | Zeile 30: | ||
[[Lösung_Aufgabe_1c_SS11]] | [[Lösung_Aufgabe_1c_SS11]] | ||
| − | ====e==== | + | ====1. e==== |
Unter dem Raum <math>\mathbb{P}</math>versteht man die Menge aller Punkte. Die Punktmenge | Unter dem Raum <math>\mathbb{P}</math>versteht man die Menge aller Punkte. Die Punktmenge | ||
<math>\varepsilon \subset \mathbb{P}</math> sei eine Ebene. Gegeben sei ferner <math>\ Q</math> mit <math>Q \in \mathbb{P} \land Q \not \in \varepsilon</math>. Definieren Sie die Begriffe Halbraum <math>\varepsilon Q^+</math> und <math>\varepsilon Q^-</math>. | <math>\varepsilon \subset \mathbb{P}</math> sei eine Ebene. Gegeben sei ferner <math>\ Q</math> mit <math>Q \in \mathbb{P} \land Q \not \in \varepsilon</math>. Definieren Sie die Begriffe Halbraum <math>\varepsilon Q^+</math> und <math>\varepsilon Q^-</math>. | ||
| − | ====f==== | + | |
| + | [[Lösung_Aufgabe_1e_SS11]] | ||
| + | |||
| + | ====1. f==== | ||
Definieren Sie den Begriff regelmäßiges Sechseck. Der Begriff n-Eck sei bereits | Definieren Sie den Begriff regelmäßiges Sechseck. Der Begriff n-Eck sei bereits | ||
definiert. | definiert. | ||
| + | |||
| + | |||
| + | [[Lösung_Aufgabe_1f_SS11]] | ||
| + | |||
===Aufgabe 2=== | ===Aufgabe 2=== | ||
| − | ====a==== | + | ====2. a==== |
Es sei <math>gQ^+ \subset \varepsilon</math> eine offene Halbebene der Ebene <math>\varepsilon</math>. Es gelte<math> P \in gQ^+</math> . Man beweise:<math> A \in gQ^+ \Rightarrow A \in gP^+</math>. (Skizzen helfen) | Es sei <math>gQ^+ \subset \varepsilon</math> eine offene Halbebene der Ebene <math>\varepsilon</math>. Es gelte<math> P \in gQ^+</math> . Man beweise:<math> A \in gQ^+ \Rightarrow A \in gP^+</math>. (Skizzen helfen) | ||
| + | |||
| + | [[Lösung_Aufgabe_2a_SS11]] | ||
[[Kategorie:Einführung_Geometrie]] | [[Kategorie:Einführung_Geometrie]] | ||
| − | ====b==== | + | |
| + | ====2. b==== | ||
Formulieren Sie die Kontraposition der Implikation aus Teilaufgabe a). | Formulieren Sie die Kontraposition der Implikation aus Teilaufgabe a). | ||
| − | ====c==== | + | |
| + | [[Lösung_Aufgabe_2b_SS11]] | ||
| + | |||
| + | ====2. c==== | ||
Warum bedarf die Implikation aus Teilaufgabe b) keines Beweises mehr? | Warum bedarf die Implikation aus Teilaufgabe b) keines Beweises mehr? | ||
| − | ====d==== | + | |
| + | [[Lösung_Aufgabe_2c_SS11]] | ||
| + | |||
| + | ====2. d==== | ||
Wir wissen bereits, dass Halbebenen konvexe Punktmengen sind. Begründen Sie, dass das Innere eines Winkels immer eine konvexe Punktmenge ist. Sie dürfen in Ihrer Begründung auf Sätze aus der Vorlesung verweisen, ohne diese noch einmal beweisen zu müssen. (Tabu ist diesbezüglich natürlich der Satz ''Das Innere eines Winkels ist konvex''.) | Wir wissen bereits, dass Halbebenen konvexe Punktmengen sind. Begründen Sie, dass das Innere eines Winkels immer eine konvexe Punktmenge ist. Sie dürfen in Ihrer Begründung auf Sätze aus der Vorlesung verweisen, ohne diese noch einmal beweisen zu müssen. (Tabu ist diesbezüglich natürlich der Satz ''Das Innere eines Winkels ist konvex''.) | ||
| − | ====e==== | + | |
| + | [[Lösung_Aufgabe_2d_SS11]] | ||
| + | |||
| + | ====2. e==== | ||
Beweisen Sie: Jede Strecke <math>\overline{AB}</math> hat höchstens einen Mittelpunkt. | Beweisen Sie: Jede Strecke <math>\overline{AB}</math> hat höchstens einen Mittelpunkt. | ||
| + | |||
| + | [[Lösung_Aufgabe_2e_SS11]] | ||
| + | |||
==Die Probeklausur vom letzten Semester== | ==Die Probeklausur vom letzten Semester== | ||
| + | ===als PDF=== | ||
| + | {{pdf|Probeklausur_SoSe_11_(1).pdf |alte Probeklausur}} | ||
== Aufgabe 1 == | == Aufgabe 1 == | ||
Aktuelle Version vom 17. Juli 2011, 12:50 Uhr
Inhaltsverzeichnis |
Bemerkungen vorab
Die Probeklausuren sind geschrieben. Das Bild, das sich dabei bei einigen Kommilitonen bot, ist erschreckend. Wer nach der Intensität, mit der wir auf den Begriffen Strecke oder Inneres eines Winkels herumgeritten sind, nicht ad hoc auch ohne explizite Vorbereitung eine entsprechende Definition anbieten kann, hat definitiv nicht verstanden, wie und in welcher Form Mathematik gelernt werden muss.--*m.g.* 18:47, 26. Jun. 2011 (CEST)
Die Klausur als PDF
Die Klausuraufgaben zum Diskutieren
Aufgabe 1
1. a
Definieren Sie den Begriff offene Strecke 
1. b
Definieren Sie, was man unter dem Kreis 
mit dem Radius 
und dem Mittelpunkt
versteht.
1. c
Definieren Sie den Begriff Inneres eines Kreises.
1. d
Was ist an der folgenden Definition nicht korrekt?
Definition (gleichschenkliges Dreieck):
- Wenn ein Dreieck zueinander kongruente Basiswinkel hat, so ist es gleichschenklig.
1. e
Unter dem Raum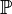 
versteht man die Menge aller Punkte. Die Punktmenge
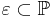sei eine Ebene. Gegeben sei ferner 
mit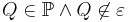 
. Definieren Sie die Begriffe Halbraum 
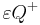und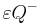 
.
1. f
Definieren Sie den Begriff regelmäßiges Sechseck. Der Begriff n-Eck sei bereits definiert.
Aufgabe 2
2. a
Es sei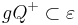 
eine offene Halbebene der Ebene 
. Es gelte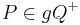
. Man beweise:
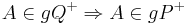. (Skizzen helfen)
2. b
Formulieren Sie die Kontraposition der Implikation aus Teilaufgabe a).
2. c
Warum bedarf die Implikation aus Teilaufgabe b) keines Beweises mehr?
2. d
Wir wissen bereits, dass Halbebenen konvexe Punktmengen sind. Begründen Sie, dass das Innere eines Winkels immer eine konvexe Punktmenge ist. Sie dürfen in Ihrer Begründung auf Sätze aus der Vorlesung verweisen, ohne diese noch einmal beweisen zu müssen. (Tabu ist diesbezüglich natürlich der Satz Das Innere eines Winkels ist konvex.)
2. e
Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt.
Die Probeklausur vom letzten Semester
als PDF
Aufgabe 1
a) Definieren Sie den Begriff: "Konkave Punktmenge" ohne den Begriff "konvex" zu gebrauchen.
b) Begründen Sie, dass der Schnitt einer offenen Halbebene E mit einer Halbgeraden, die zwei Punkte mit E gemeinsam hat, auf jeden Fall eine konvexe Punktmenge ist.
c) Zeigen Sie an einem Beispiel, dass die Vereinigungsmenge des Inneren zweier Drachenvierecke, die keine Rauten sind, konkav sein kann.
Aufgabe 2
Es seien A und B zwei verschiedene Punkte. Welche Ergebnisse erzielen Sie nach den folgenden Mengenoperationen?
a)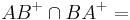 
b)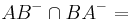 
c)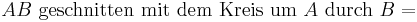 
d)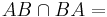
Aufgabe 3
Wir gehen von folgender Implikation aus: Wenn ein Punkt P zur Mittelsenkrechten der Strecke gehört, dann hat er zu den Punkten A und B ein und denselben Abstand.
a) Formulieren Sie die Kontraposition dieser Implikation.
b) Formulieren Sie die Umkehrung dieser Implikation.
Aufgabe 4
Definieren Sie den Begriff Strahl 
. Verwenden Sie dabei den Begriff Strecke.
Aufgabe 5
Definition (gemeiner Dreiecksschneider): Unter einem gemeinen Dreieckschneider versteht man eine Gerade, die alle drei offenen Seiten eines Dreiecks schneidet.
Beschreiben Sie die Menge aller gemeinen Dreiecksschneider und begründen Sie Ihre Aussage.
Aufgabe 6
Es seien A, B und C drei paarweise verschiedene Punkte. Beweisen Sie:
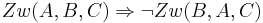
Aufgabe 7
Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:
