Peripheriewinkelsatz und Zentriwinkel-Peripheriewinkelsatz (SoSe 11): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Definition XIX.2 (Zentriwinkel))
(→‎Definition XIX.1 (Peripheriewinkel))
 
(14 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
=Videos=
 +
==Peripheriewinkelsatz==
 +
===Begriff de3s Peripheriewinkels===
 +
{{#ev:youtube|7J9vZGf9Lps}}
 +
===Peripheriewinkelsatz===
 +
{{#ev:youtube|0tsVjlH7Da8}}
 +
==Satz des Thales==
 +
=== Satzfindung ===
 +
{{#ev:youtube|5Hli03ctSX4}}
 +
=== "Beweisen" am Beispiel ===
 +
{{#ev:youtube|o_gbIikyHuw}}
 +
=== Ikonischer Beweis ===
 +
{{#ev:youtube|Av0LDOuvZzQ}}
 +
 
==Definition XIX.1 (Peripheriewinkel)==  
 
==Definition XIX.1 (Peripheriewinkel)==  
 
Der Winkel <math> \angle ACB </math> im nachfolgenden Applet ist ein Peripheriewinkel. Definieren Sie diesen Begriff:<br /><br />
 
Der Winkel <math> \angle ACB </math> im nachfolgenden Applet ist ein Peripheriewinkel. Definieren Sie diesen Begriff:<br /><br />
  
−
Wenn der Scheitelpunkt C eines Winkels <math> \angle ACB </math> auf einem Kreis k liegt, dann ist der Winkel ein Peripheriewinkel. --[[Benutzer:Teufelchen|Teufelchen]] 16:28, 17. Jul. 2011 (CEST)<br /><br />
+
Wenn der Scheitelpunkt C eines Winkels <math> \angle ACB </math> auf einem Kreis k liegt, dann ist der Winkel ein Peripheriewinkel. --[[Benutzer:Teufelchen|Teufelchen]] 16:28, 17. Jul. 2011 (CEST)<br /> Dann könnten die Schenkel des Winkels auch außerhalb des Inneren des Kreises k liegen.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 16:15, 24. Jul. 2011 (CEST)<br />
 +
<br />
 +
Wenn der Scheitelpunkt C eines Winkels <math> \angle ACB </math> auf einem Kreis k liegt und seine beiden Schenkel denselben Kreis schneiden, dann ist der Winkel ein Peripheriwinkel.--[[Benutzer:Prayush|Prayush]] 21:21, 17. Jul. 2011 (CEST)
 +
<br />ganz wichtig: ... ein '''Peripheriewinkel des Kreises k'''! (Erklärung von m.g. unter Zentriwinkel)--[[Benutzer:Tutorin Anne|Tutorin Anne]] 16:15, 24. Jul. 2011 (CEST)
  
 
==Definition XIX.2 (Zentriwinkel)==  
 
==Definition XIX.2 (Zentriwinkel)==  
 
Der Winkel <math> \angle AMB </math> im nachfolgenden Applet ist ein Zentriwinkel. Definieren Sie diesen Begriff:<br /><br />
 
Der Winkel <math> \angle AMB </math> im nachfolgenden Applet ist ein Zentriwinkel. Definieren Sie diesen Begriff:<br /><br />
  
−
Wenn der Scheitelpunkt M eines Winkels <math> \angle AMB </math> der Mittelpunkt eines Kreises k ist, dann ist der Winkel ein Zentriwinkel. --[[Benutzer:Teufelchen|Teufelchen]] 16:31, 17. Jul. 2011 (CEST)<br /><br />
+
Wenn der Scheitelpunkt M eines Winkels <math> \angle AMB </math> der Mittelpunkt eines Kreises k ist, dann ist der Winkel ein Zentriwinkel. ''Dieser Kreis sei ein Umkreis eines Dreiecks <math>\overline{ABC}</math>'' --[[Benutzer:Teufelchen|Teufelchen]] 16:31, 17. Jul. 2011 (CEST)<br /><br /> Das Kursive wurde nachträglcih eingefügt. --[[Benutzer:Teufelchen|Teufelchen]] 22:46, 17. Jul. 2011 (CEST)<br /><br />
  
 
<u>Bemerkung m.g.:</u> <br />
 
<u>Bemerkung m.g.:</u> <br />
 
::Nach der Definition wäre jeder Winkel ein Zentriwinkel. Der Begriff macht erst Sinn, wenn er als Relationsbegriff aufgefasst wird: Ein bestimmter Winkel ist ''Zentriwinkel von einem bestimmten Kreis''.--[[Benutzer:*m.g.*|*m.g.*]] 18:19, 17. Jul. 2011 (CEST)
 
::Nach der Definition wäre jeder Winkel ein Zentriwinkel. Der Begriff macht erst Sinn, wenn er als Relationsbegriff aufgefasst wird: Ein bestimmter Winkel ist ''Zentriwinkel von einem bestimmten Kreis''.--[[Benutzer:*m.g.*|*m.g.*]] 18:19, 17. Jul. 2011 (CEST)
 +
 +
Definition (Zentriwinkel): Es sei ABC ein Dreieck und M der Mittelpunkt seines Umkreises k. Jeder Winkel mit Scheitelpunkt M heißt Zentriwinkel des Kreises k.
 +
 +
Ist das so richtig, oder ist nur der Winkel AMB Zentriwinkel? --[[Benutzer:...s...|...s...]] 17:48, 23. Jul. 2011 (CEST)
  
 
<ggb_applet width="466" height="399"  version="3.2" ggbBase64="UEsDBBQACAAIADGnPT4AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1Vnbcts2EH1uvoLDd9G4g5yRkpHd6Uxm4qYTp3noG0VCEmqKVEnIlvxXmf5Hv6kLgNTVUa04dSK/0FxAi8U5e3YBqf9mOSuCO1U3uioHIY5QGKgyq3JdTgbhwox7cfjm9av+RFUTNarTYFzVs9QMQhqR0NoX+vWrn/rNtLoP0sJN+aTV/SAcp0WjwqCZ1yrNm6lSZseeLpa60Gm9ej/6U2Wm2Qx4J2/L+QJWMfUCbNksf6eb7vXCLTgvtPlZ3+lc1UFRZYNQcAgd/vukaqOztBiEDHkLGYRkbxBM1I5Oq1o/VKWx0zfOx2AJgkY/KECEWFv/wm20rxZZoXOdlnYzLg6YFAT3OjdTWFAIcKn0ZGoBSqT3llVVnd+sGqNmwfIPVVeDUDKL88q/UOxQbyAsWI8jN7T95ryouxtlDLDSBOlSbfCa1DrfeXnbXFbFxjSvdGmu0rlZ1I5S2ppuzMouAGvVNt5hOSlUayOA+FRlt6NqeeMxoN71x9XcfcQFNJpcVUVVB7VFl8OE9jnyTzfHRrqehdwc5Ga0PqzT9ThOiJvhniP/dLMKXfrQ2p3jbtcYdcvoJrAGCyNk4nrzRTpSwGwYLEpt3nUvkAG37Vax/8Cvi9kIJLCdA2uf+Fv57F/sZU//VtWlKnyOlMDtolo0wZ3NRb+WCyRXmZ7Bqx9oIUktXb9DAN6aq0mtusC9gDxgbhRt5+GeuX/RBWFjaCDWzEAlgP0YuxcrVAMiGYQ32bTUdTYNgzw1dsSqoVAzBVIxLi9cWq3xuQ7XdaFyEu/E3I5vkIbhR3PEZVNazKcpWDoZFOkKBL+9Lefvusp3N5uWAJrbCehubh1YWuZKeUZNm8nBHBw6XWwh7oBqgqUtcgy0aMtiAsp+8PXRzfEasuJ3q9KWYA/If0DzyyE0u7l1FtiQCHlwWMTIaeBk1WyWlnlQpjNY6QrSqlAOE22rfpAimz5Bii1UHoaF6QZuvbPWxQHSkMQ6WwN5G+7WDzMFmZaqaVyRM9vl7DmZip7MxfvxuFHGwtejxKHXw+QYV0+KHTqOKu8g8qpugmCJ2j6+Qj6g4KGzLAHSnm8wuDU94C3iIC1qvQyG3fxhN2sIDVNGHCGabP7ATNsVhszuyKplyO2erF58aH+VPvzGF0dIs0yPgaKjKfGb08tuRtwepMLV8VTYFd3VV9UjTHxnc88fQ3dw8OIsRoQynCDCqZCtCqWQmDNJKMFSEPocST4N/+Ep+A9fHP8treHEYfQC7KBIYoISnsQCJQQL3DUQTCWPsUBSxCzBLP7/6bk8hZ7L70iP8BC9ADs8igF/IAdkgyRBiPu8iAQFzihhCYlpwixpX8/Oh3S1x82Vb2bDA4rS4xTV4KkjIP0WrWwLlOf3sgOOtmuUIAmXcLPhgKpEsVdBj0ScwaugHLSAQBG+SqGIIplQzCl8hHEOVeyU7rfXYvQM7oaZNmu0C5sRb0sDp3HlTreHh+xbpeb2dvO+/FinZWMvuX7O1uH9VLovD+gePZ3u0TnRzaC6CYIwkzShVMTYsU0gCQjikmMsEVyNvah6hMPhgBBpqyTDmODzodpdkvfIHnqyLefkMc7/+fs46e4mt2YMZtvPQzyLFmzoHBJaCUoEjyVlnJDnnFcxOqQdP5H2U4hK62yrXnbGoqjuP6hxoZYOyafCfqMm1v448IeIZ8cBb1pvHVzZOSkNwRlcCGhSPGYIJZAQTmo8woJJQWMBauNwSPdSExGhAkP1RQzLGHR4PlI7yvn1Aef5aZzn58Q5XNhiQhiGkwmBHoliTrr6GssEMYRpgmRMY94W2AguAUhAJaY0jpFk58769ZeUrk5jXZ0T6ziiBMgFQSMJ1wYei5Z0tnuC9d9L9ZIIzk6gcyI4R0zig69Of1zSj3TV6y921c8nddXP+12VRJQTHGM4dEomAGf2sl11c/nxt/ce/d4t92L761/3g0f7i8/rfwFQSwcIHuZo3L0FAAAjGgAAUEsBAhQAFAAIAAgAMac9Ph7maNy9BQAAIxoAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAD3BQAAAAA=" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" />
 
<ggb_applet width="466" height="399"  version="3.2" ggbBase64="UEsDBBQACAAIADGnPT4AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1Vnbcts2EH1uvoLDd9G4g5yRkpHd6Uxm4qYTp3noG0VCEmqKVEnIlvxXmf5Hv6kLgNTVUa04dSK/0FxAi8U5e3YBqf9mOSuCO1U3uioHIY5QGKgyq3JdTgbhwox7cfjm9av+RFUTNarTYFzVs9QMQhqR0NoX+vWrn/rNtLoP0sJN+aTV/SAcp0WjwqCZ1yrNm6lSZseeLpa60Gm9ej/6U2Wm2Qx4J2/L+QJWMfUCbNksf6eb7vXCLTgvtPlZ3+lc1UFRZYNQcAgd/vukaqOztBiEDHkLGYRkbxBM1I5Oq1o/VKWx0zfOx2AJgkY/KECEWFv/wm20rxZZoXOdlnYzLg6YFAT3OjdTWFAIcKn0ZGoBSqT3llVVnd+sGqNmwfIPVVeDUDKL88q/UOxQbyAsWI8jN7T95ryouxtlDLDSBOlSbfCa1DrfeXnbXFbFxjSvdGmu0rlZ1I5S2ppuzMouAGvVNt5hOSlUayOA+FRlt6NqeeMxoN71x9XcfcQFNJpcVUVVB7VFl8OE9jnyTzfHRrqehdwc5Ga0PqzT9ThOiJvhniP/dLMKXfrQ2p3jbtcYdcvoJrAGCyNk4nrzRTpSwGwYLEpt3nUvkAG37Vax/8Cvi9kIJLCdA2uf+Fv57F/sZU//VtWlKnyOlMDtolo0wZ3NRb+WCyRXmZ7Bqx9oIUktXb9DAN6aq0mtusC9gDxgbhRt5+GeuX/RBWFjaCDWzEAlgP0YuxcrVAMiGYQ32bTUdTYNgzw1dsSqoVAzBVIxLi9cWq3xuQ7XdaFyEu/E3I5vkIbhR3PEZVNazKcpWDoZFOkKBL+9Lefvusp3N5uWAJrbCehubh1YWuZKeUZNm8nBHBw6XWwh7oBqgqUtcgy0aMtiAsp+8PXRzfEasuJ3q9KWYA/If0DzyyE0u7l1FtiQCHlwWMTIaeBk1WyWlnlQpjNY6QrSqlAOE22rfpAimz5Bii1UHoaF6QZuvbPWxQHSkMQ6WwN5G+7WDzMFmZaqaVyRM9vl7DmZip7MxfvxuFHGwtejxKHXw+QYV0+KHTqOKu8g8qpugmCJ2j6+Qj6g4KGzLAHSnm8wuDU94C3iIC1qvQyG3fxhN2sIDVNGHCGabP7ATNsVhszuyKplyO2erF58aH+VPvzGF0dIs0yPgaKjKfGb08tuRtwepMLV8VTYFd3VV9UjTHxnc88fQ3dw8OIsRoQynCDCqZCtCqWQmDNJKMFSEPocST4N/+Ep+A9fHP8treHEYfQC7KBIYoISnsQCJQQL3DUQTCWPsUBSxCzBLP7/6bk8hZ7L70iP8BC9ADs8igF/IAdkgyRBiPu8iAQFzihhCYlpwixpX8/Oh3S1x82Vb2bDA4rS4xTV4KkjIP0WrWwLlOf3sgOOtmuUIAmXcLPhgKpEsVdBj0ScwaugHLSAQBG+SqGIIplQzCl8hHEOVeyU7rfXYvQM7oaZNmu0C5sRb0sDp3HlTreHh+xbpeb2dvO+/FinZWMvuX7O1uH9VLovD+gePZ3u0TnRzaC6CYIwkzShVMTYsU0gCQjikmMsEVyNvah6hMPhgBBpqyTDmODzodpdkvfIHnqyLefkMc7/+fs46e4mt2YMZtvPQzyLFmzoHBJaCUoEjyVlnJDnnFcxOqQdP5H2U4hK62yrXnbGoqjuP6hxoZYOyafCfqMm1v448IeIZ8cBb1pvHVzZOSkNwRlcCGhSPGYIJZAQTmo8woJJQWMBauNwSPdSExGhAkP1RQzLGHR4PlI7yvn1Aef5aZzn58Q5XNhiQhiGkwmBHoliTrr6GssEMYRpgmRMY94W2AguAUhAJaY0jpFk58769ZeUrk5jXZ0T6ziiBMgFQSMJ1wYei5Z0tnuC9d9L9ZIIzk6gcyI4R0zig69Of1zSj3TV6y921c8nddXP+12VRJQTHGM4dEomAGf2sl11c/nxt/ce/d4t92L761/3g0f7i8/rfwFQSwcIHuZo3L0FAAAjGgAAUEsBAhQAFAAIAAgAMac9Ph7maNy9BQAAIxoAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAD3BQAAAAA=" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" />
 +
<br /><br />
 +
Auch die anderen Winkel sind Zentriwinkel des Kreises k. Es gibt mehrere und unterschiedlich große Zentriwinkel in einem Kreis. <br />
 +
Wie könnte man Zentriwinkel eines Kreises noch definieren, ohne ein Dreieck zu nutzen?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 16:18, 24. Jul. 2011 (CEST)<br />
  
 
==Idee des Beweises eines Spezialfalls ==
 
==Idee des Beweises eines Spezialfalls ==
Zeile 24: Zeile 48:
  
 
== Der Zentri-Peripheriewinkelsatz ==
 
== Der Zentri-Peripheriewinkelsatz ==
−
ergänzen Sie:
+
ergänzen Sie: <br />
 +
Jeder Peripheriewinkel ist halb so groß wie sein zugehöriger Zentriwinkel.--[[Benutzer:Zeqiraj|Zeqiraj]] 19:40, 17. Jul. 2011 (CEST)
 +
<br />Was ist ein zugehöriger Zentriwinkel?<br />
 +
<ggb_applet width="328" height="321"  version="3.2" ggbBase64="UEsDBBQACAAIAJeA+D4AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VjNcts2ED43T4Hh3TR++DsjOSOrF8/EdSdOc8gNIiEJNUWqIGhLfp6+QPMKveeZugBIiZJsxU46k9i2Z2gulovF9+23ADl4u1oU6FaoWlbl0CM+9pAosyqX5WzoNXp6knhvz94MZqKaiYniaFqpBddDj/nUM/ZGnr35ZVDPqzvEC+vyUYq7oTflRS08VC+V4Hk9F0Lv2HmzkoXkan01+VNkut4OuCAX5bKBWbRqwJYt8ney7m5P7YTLQupf5a3MhUJFlQ29KITU4b+PQmmZ8WLoBdhZ6NCje4NgYmZ0Xil5X5XauG+DF3wiCgDgWq8LgdCtGWVuaArOCNXyXgBY1NgGpxaDgWiyQuaSl2adNkVwQuhO5noOj9MEZhNyNjfYkdRFy6pK5dfrWosFWn0Sqhp6J4QkhoS1uyVxZO5qyBlmDLEd6t/ZOOL2WmgNGdeIr8QWzJmS+c7NRX1eFVvTspKlHvOlbpTlm7Umu/ChB3Mpk/GonBWitRGgYy6ym0m1unYoMBf6w3ppH7EJTWbjqqgUUgb6EBza68RdrY/JdOOFrQ+2Hm0ME3QzTlJqPex14q6OK1m61NqVk27VBHfTyBoZg4ERynSzeMvy0PNQU0r9rruB8rjZLtU88FuzmIA++gWyiUn+r5iD0736GdwIVYrCVUkJ3DZVU7tSdHPZRHKRyQXcuoEWEm7o+gMScNZczJToEnfqcoDZUdyvxD3z4LRLwuRQQ66ZhjYB69FmLUbFGhQ09EZlKdCnf/+emzISykM518bByKIQCwGa0bY8bHVtYLr0Nr2jsm2gE3w7vgUchh8sFVtUvFjOOVg6NRR8DU2hvzob77LKd9fMS8DOLggEuDQBDDtLIfK2Eeq2pNESQlqB9KC3iNVoBTr0wwBUaQJAcd67h62PE5PpA9seAkw7SL4CzvlrAYc4cKifRs9DJ6sWC17mqOQLmGksVVYIC4o0mwPi2FQQ4sRg5YBodDeQuWBtiAOooZxltoEy83Y7iZ6DYEtR10ZSm4WeHuejt/rHCMHfTseTkoPtRZS3kFqlaoRWuGVqjd2E6L6zrACzE7eXkNZ0T3rMAPNKrtCo8x91XiOzlwKTIUu3PzHYWTvFKIDIThCj0E7SNiXxV+nyr10jhFLK5FRmx0n/3Upil/PsgOzxcbJ3dTX+Jl0R6nYxe/1ZtBX7ESaM0IhQmtA0ZVZoJ8SP4iQIA8pClkQpJd+lu6dRMHoOBaPXQ0HiM2AgiYIkDkkYxu0+EKQhJmnCUpzGASbP3BZ2CXjP13vwjx7revw4CwoidRjzn7/nbVE+oX4QBWmCSYRTTMM0CV2pM5/EPfijNLRIQ4vCEY3giA9/SRgEwXO66F6nkgt418ik3qBdmHq4KDUc4IQ9EB2ey26EWJoD8VX5QfGyNi9Nzqd33nsu3eMDuidPp3vykuimhtUAhBMHQRIw2vY17MfwchQz4JoyGsaurZ2QGOwRwSwiYZwyisOXTPajJ5r86WTnL4ls0LZh0hEMr+z9H9buXKHPYtw7ciSvgOFDOYunMyxeEsPETw7OI/aFAEc7pxfa6hn7CUmSFH6jEGMSvCA92y8le3yfO75NF6cP0f7ln+O829f5DWngbZ6HfJoWb+KnJIgpjVMKW14cs/hrxB97dST4kHlylPmr6bQW2kqZtZ06frAwDr7YHOGRq6x3QOqMRVHdvRfTQqws0N/DytixculYOWy3Xz4/i5XP+6zAiSVkMUuBmCikOPhhnBDcHpXIjybltP8RyX44bT8qn/0HUEsHCH1w4JwxBQAAhhYAAFBLAQIUABQACAAIAJeA+D59cOCcMQUAAIYWAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAawUAAAAA" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" />--[[Benutzer:Tutorin Anne|Tutorin Anne]] 16:25, 24. Jul. 2011 (CEST)
 +
 
 +
<br /><br />
 +
 
 +
Jeder Zentriwinkel über einem Kreisbogen ist doppelt so groß wie der dazugehörige Peripheriewinkel. --[[Benutzer:Muffinkopf|Muffinkopf]] 15:45, 24. Jul. 2011 (CEST)<br />
 +
Bei dieser Formulierung ist auch kritisch, dass "Zentriwinkel über einem Kreisbogen" nicht definiert wurde.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 16:25, 24. Jul. 2011 (CEST)
 +
<br />
 +
 +
Wie heißt der Satz denn jetzt richtig?--[[Benutzer:Verteidigungswolf|Verteidigungswolf]] 09:48, 26. Jul. 2011 (CEST)
  
 
=== Satz XIX.1:(Der Zentri-Peripheriewinkelsatz) ===
 
=== Satz XIX.1:(Der Zentri-Peripheriewinkelsatz) ===
Zeile 32: Zeile 67:
 
=== Satz XIX.2:(Der Peripheriewinkelsatz) ===
 
=== Satz XIX.2:(Der Peripheriewinkelsatz) ===
 
ergänzen Sie:
 
ergänzen Sie:
 +
Alle Peripheriewinkel über derselben Sehne sind kongruent zueinander.--[[Benutzer:Zeqiraj|Zeqiraj]] 19:39, 17. Jul. 2011 (CEST)
 +
[[Kategorie:Einführung_Geometrie]]<br />
 +
Was bedeutet "über" ?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 16:26, 24. Jul. 2011 (CEST)
  
−
[[Kategorie:Einführung_Geometrie]]
+
Es seien A und B zwei Punkte des Kreises k. Für alle C, die sich bezüglich AB in einer Halbebene befinden und C Element k gilt: Winkel ACB ist immer gleich groß.--[[Benutzer:Verteidigungswolf|Verteidigungswolf]] 09:58, 26. Jul. 2011 (CEST)

Aktuelle Version vom 26. Juli 2011, 16:18 Uhr

Inhaltsverzeichnis

Videos

Peripheriewinkelsatz

Begriff de3s Peripheriewinkels

Peripheriewinkelsatz

Satz des Thales

Satzfindung

"Beweisen" am Beispiel

Ikonischer Beweis

Definition XIX.1 (Peripheriewinkel)

Der Winkel 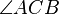\angle ACB im nachfolgenden Applet ist ein Peripheriewinkel. Definieren Sie diesen Begriff:

Wenn der Scheitelpunkt C eines Winkels 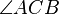\angle ACB auf einem Kreis k liegt, dann ist der Winkel ein Peripheriewinkel. --Teufelchen 16:28, 17. Jul. 2011 (CEST)
Dann könnten die Schenkel des Winkels auch außerhalb des Inneren des Kreises k liegen.--Tutorin Anne 16:15, 24. Jul. 2011 (CEST)

Wenn der Scheitelpunkt C eines Winkels 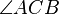\angle ACB auf einem Kreis k liegt und seine beiden Schenkel denselben Kreis schneiden, dann ist der Winkel ein Peripheriwinkel.--Prayush 21:21, 17. Jul. 2011 (CEST)
ganz wichtig: ... ein Peripheriewinkel des Kreises k! (Erklärung von m.g. unter Zentriwinkel)--Tutorin Anne 16:15, 24. Jul. 2011 (CEST)

Definition XIX.2 (Zentriwinkel)

Der Winkel 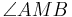\angle AMB im nachfolgenden Applet ist ein Zentriwinkel. Definieren Sie diesen Begriff:

Wenn der Scheitelpunkt M eines Winkels 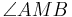\angle AMB der Mittelpunkt eines Kreises k ist, dann ist der Winkel ein Zentriwinkel. Dieser Kreis sei ein Umkreis eines Dreiecks \overline{ABC} --Teufelchen 16:31, 17. Jul. 2011 (CEST)

Das Kursive wurde nachträglcih eingefügt. --Teufelchen 22:46, 17. Jul. 2011 (CEST)

Bemerkung m.g.:

Nach der Definition wäre jeder Winkel ein Zentriwinkel. Der Begriff macht erst Sinn, wenn er als Relationsbegriff aufgefasst wird: Ein bestimmter Winkel ist Zentriwinkel von einem bestimmten Kreis.--*m.g.* 18:19, 17. Jul. 2011 (CEST)

Definition (Zentriwinkel): Es sei ABC ein Dreieck und M der Mittelpunkt seines Umkreises k. Jeder Winkel mit Scheitelpunkt M heißt Zentriwinkel des Kreises k.

Ist das so richtig, oder ist nur der Winkel AMB Zentriwinkel? --...s... 17:48, 23. Jul. 2011 (CEST)



Auch die anderen Winkel sind Zentriwinkel des Kreises k. Es gibt mehrere und unterschiedlich große Zentriwinkel in einem Kreis.
Wie könnte man Zentriwinkel eines Kreises noch definieren, ohne ein Dreieck zu nutzen?--Tutorin Anne 16:18, 24. Jul. 2011 (CEST)

Idee des Beweises eines Spezialfalls

Um welchen Spezialfall handelt es sich?
Können Sie einen formalen Beweis aus dem Video ableiten?



Der Zentri-Peripheriewinkelsatz

ergänzen Sie:
Jeder Peripheriewinkel ist halb so groß wie sein zugehöriger Zentriwinkel.--Zeqiraj 19:40, 17. Jul. 2011 (CEST)
Was ist ein zugehöriger Zentriwinkel?

--Tutorin Anne 16:25, 24. Jul. 2011 (CEST)



Jeder Zentriwinkel über einem Kreisbogen ist doppelt so groß wie der dazugehörige Peripheriewinkel. --Muffinkopf 15:45, 24. Jul. 2011 (CEST)
Bei dieser Formulierung ist auch kritisch, dass "Zentriwinkel über einem Kreisbogen" nicht definiert wurde.--Tutorin Anne 16:25, 24. Jul. 2011 (CEST)

Wie heißt der Satz denn jetzt richtig?--Verteidigungswolf 09:48, 26. Jul. 2011 (CEST)

Satz XIX.1:(Der Zentri-Peripheriewinkelsatz)

Der Peripheriewinkelsatz

Satz XIX.2:(Der Peripheriewinkelsatz)

ergänzen Sie: Alle Peripheriewinkel über derselben Sehne sind kongruent zueinander.--Zeqiraj 19:39, 17. Jul. 2011 (CEST)
Was bedeutet "über" ?--Tutorin Anne 16:26, 24. Jul. 2011 (CEST)

Es seien A und B zwei Punkte des Kreises k. Für alle C, die sich bezüglich AB in einer Halbebene befinden und C Element k gilt: Winkel ACB ist immer gleich groß.--Verteidigungswolf 09:58, 26. Jul. 2011 (CEST)

Von „http://geometrie.zum.de/index.php?title=Peripheriewinkelsatz_und_Zentriwinkel-Peripheriewinkelsatz_(SoSe_11)&oldid=8509“