Lösung von Aufg. 12.3 SS11: Unterschied zwischen den Versionen
HecklF (Diskussion | Beiträge) |
HecklF (Diskussion | Beiträge) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 68: | Zeile 68: | ||
Wichtig ist, dass man den zweiten Fall nicht vergisst!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 10:29, 17. Jul. 2011 (CEST) | Wichtig ist, dass man den zweiten Fall nicht vergisst!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 10:29, 17. Jul. 2011 (CEST) | ||
| − | <br /> | + | <br /><br /><br /> |
Wie schaut es denn damit aus: Fall eins schenke ich mir aus Zeitgründen, dass P=M ist. | Wie schaut es denn damit aus: Fall eins schenke ich mir aus Zeitgründen, dass P=M ist. | ||
| − | + | <br /> | |
| + | <br /> | ||
Voraussetzung: nkoll(A,B,C), <math>\left| AC \right| = \left| BC \right|</math> <br /> | Voraussetzung: nkoll(A,B,C), <math>\left| AC \right| = \left| BC \right|</math> <br /> | ||
| Zeile 100: | Zeile 101: | ||
|} | |} | ||
| − | --[[Benutzer:HecklF|Flo60]] 15:35, 26. Jul. 2011 (CEST) | + | --[[Benutzer:HecklF|Flo60]] 15:35, 26. Jul. 2011 (CEST) --[[Benutzer:HecklF|Flo60]] 20:49, 26. Jul. 2011 (CEST) |
Aktuelle Version vom 26. Juli 2011, 19:49 Uhr
Beweisen Sie Satz VII.6 a:
- Wenn ein Punkt
 zu den Endpunkten der Strecke
zu den Endpunkten der Strecke  jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von
jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von  .
.
- Wenn ein Punkt
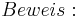
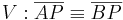
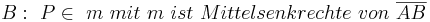
Skizze dazu: (--Tutorin Anne 17:33, 5. Jul. 2011 (CEST))
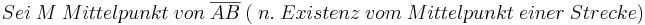
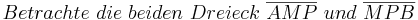
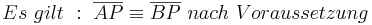
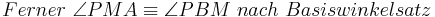 (davor sollte man noch sagen, das hier ein gleichschenkliges Dreieck vorliegt > wo sollen sonst Basiswinkel vorliegen?)
(davor sollte man noch sagen, das hier ein gleichschenkliges Dreieck vorliegt > wo sollen sonst Basiswinkel vorliegen?)
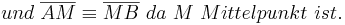
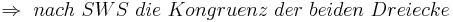
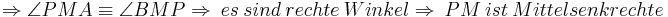
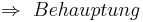 --Peterpummel 17:47, 3. Jul. 2011 (CEST)
--Peterpummel 17:47, 3. Jul. 2011 (CEST)
Der Beweis ist gut, allerdings solltest du wie Phil den 2. Fall nicht vergessen, denn dann ergeben sich ja keine Dreiecke.--Tutorin Anne 17:33, 5. Jul. 2011 (CEST)
Lösungsvorschlag 2:
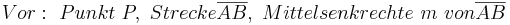

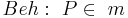
Man muss in zwei Fälle unterscheiden:
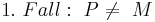
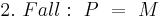
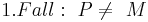
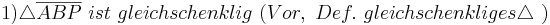
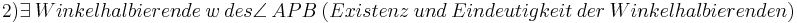
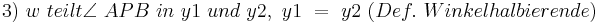
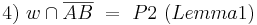
5)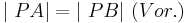
6) 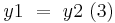 Nicht einfach Schritte oder Vorausetzung wiederholen!
Nicht einfach Schritte oder Vorausetzung wiederholen!
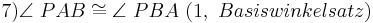
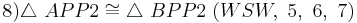
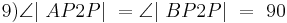 (8, Def. Nebenwinkel, Supplementaxiom)
(8, Def. Nebenwinkel, Supplementaxiom)
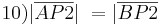 (8)
(8)
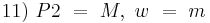 (10, Def. Mittelpunkt, 9, Def. Mittelsenkrechte)
(10, Def. Mittelpunkt, 9, Def. Mittelsenkrechte)
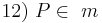 (9, 10, 11)
(9, 10, 11)
Ich denke, auch so kann Fall I beweisen werden. Scheint mir aufwendiger, aber auch richtig. Gut!--Tutorin Anne 17:57, 5. Jul. 2011 (CEST)
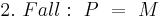
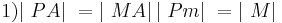 (Annahme 2. Fall) (Hier verstehe ich nicht, was du damit zeigen willst. --Tutorin Anne 17:57, 5. Jul. 2011 (CEST))
(Annahme 2. Fall) (Hier verstehe ich nicht, was du damit zeigen willst. --Tutorin Anne 17:57, 5. Jul. 2011 (CEST))
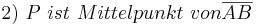 (Def. Mittelpunkt, 1)
(Def. Mittelpunkt, 1)
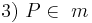 (2, Def. Mittelsenkrechte)---phil- 15:04, 5. Jul. 2011 (CEST)
(2, Def. Mittelsenkrechte)---phil- 15:04, 5. Jul. 2011 (CEST)
zum 2. Fall:
zu zeigen ist ja hier nur, dass P Element der Mittelsenkrechten ist:
da P=M ist PA = PB (die Strecken) und somit ist ja nach Def. Mittelsenkrechte erfüllt,
dass er auf m liegt. (die Gerade m durch P kann ja dann senkrecht stehen)
Oder muss man dann noch einen weiteren Punkt außerhalb der Gerade AB annehmen, der mit
P eine Senkrechte (Ex und Eind. Senkrechte zu einem Punkt) durch AB bildet?
Bitte um einen Kommentar....danke--mm_l 10:31, 15. Jul. 2011 (CEST)
Nein das genügt für Fall 2. Es ist nicht mehr zu zeigen; das ist nur ein einfacher Schritt:
nach Definiton Mittelsenkrechte und Voraussetzung P ist Mittelpunkt von

Wichtig ist, dass man den zweiten Fall nicht vergisst!--Tutorin Anne 10:29, 17. Jul. 2011 (CEST)
Wie schaut es denn damit aus: Fall eins schenke ich mir aus Zeitgründen, dass P=M ist.
Voraussetzung: nkoll(A,B,C), 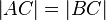
Behauptung: 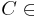 der Mittelsenkrechten von
der Mittelsenkrechten von 
Annahme: 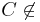 der Mittelsenkrechten
der Mittelsenkrechten
| 1 | Es existiert genau eine Gerade g mit 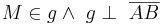 |
Nach ex. und eind. MS |
| 2 | wegen der Annahme, dass C kein Element vong ist, schneidet g das Dreieck ABC in einer weiteren Seite im Punkt D. Sei dies oBdA  |
Axiom von Pasch, Annahme, (1) |
| 3 |  |
Mittelsenkrechte Satz "=>" |
| 4 | 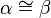 |
Nach Voraussetzung und Basiswinkelsatz (Alpha ist der Ursprüngliche Winkel um A und Beta der ursprüngliche Winkel um B |
| 5 | 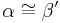 |
Nach Konstruktion (3) und Basiswinkelsatz (Beta' ist der neue Winkel um ABD |
| 6 | 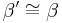 |
Rechnen in R, (4) und (5) |
| 7 | In AB,C+ existiert genau ein Winkel 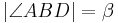 |
Winkelkonstruktionsaxiom, (6) |
| 8 | Strahl BC+ ist Identisch mit BD+ und schneidet somit AC im Punkt C und im Punkt D | (2), (7) |
| 9 | AC und BC sind identisch nach dem Satz aus der Inzidenzgeometrie und weil sie zwei gemeinsame Punkte haben, was ein WIEDERSPRUCH ist zur Annahme, dass die Punkte A, B und C nicht kollinear sind. |
--Flo60 15:35, 26. Jul. 2011 (CEST) --Flo60 20:49, 26. Jul. 2011 (CEST)

