Lösung von Aufgabe 4.1 (WS 11/12): Unterschied zwischen den Versionen
Miriam (Diskussion | Beiträge) |
|||
| (6 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
b) Fassen Sie den Basiswinkelsatz und seine Umkehrung zu einem Satz zusammen (Kriterium). | b) Fassen Sie den Basiswinkelsatz und seine Umkehrung zu einem Satz zusammen (Kriterium). | ||
<br /> | <br /> | ||
| − | + | a) Ein Dreieck, dessen Basiswinkel kongruent zueinander sind, ist ein gleichschenkliges Dreieck. | |
b) Genau dann,wenn die Basiswinkel eines Dreieckes kongruent zueinander sind, ist das Dreieck gleichschenklig.--[[Benutzer:Miriam|Miriam]] 12:35, 4. Nov. 2011 (CET) | b) Genau dann,wenn die Basiswinkel eines Dreieckes kongruent zueinander sind, ist das Dreieck gleichschenklig.--[[Benutzer:Miriam|Miriam]] 12:35, 4. Nov. 2011 (CET) | ||
| − | + | <br /> | |
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
| + | @ Miriam: Ich würde statt Basiswinkel eher Innenwinkel verwenden. | ||
| + | a) Wenn in einem Dreieck zwei beliebige Innenwinkel kongruent zueinander sind, dann ist das Dreieck gleichschenklig. | ||
| + | b) Genau dann, wenn in einem Dreieck zwei beliebige Innenwinkel kongruent zueinander sind, ist das Dreieck gleichschenklig. --[[Benutzer:Todah raba|Todah raba]] 18:24, 4. Nov. 2011 (CET) | ||
| + | |||
| + | [[Satz:]] | ||
| + | Sei ABC ein Dreieck, für das gilt, die Strecke AC ist kongruent zur Strecke BC, dann gilt Winkel BAC ist kongruent zum Winkel ABC.<br /> | ||
| + | Wozu steht dieser Satz hier? Zu welcher (Teil)aufgabe gehört er? --[[Benutzer:Tutorin Anne|Tutorin Anne]] 15:16, 8. Nov. 2011 (CET)<br /> | ||
| + | Und, wer hat den Satz hier reingestellt? Bitte immer die Signatur mit angeben, damit jeder Leser zwischen Aufgaben, Skript und studentischen Beiträgen unterscheiden kann, danke!--[[Benutzer:Schnirch|Schnirch]] 14:11, 10. Nov. 2011 (CET) | ||
| + | |||
| + | AC = BC «» Winkel BAC = Winkel ABC (Aquivalenz, wenn Aussage rechts wahr ist, ist auch Aussage links wahr und umgekehrt.)--[[Benutzer:Costa rica|Costa rica]] 15:25, 7. Nov. 2011 (CET) | ||
| + | <br />An dieser Stelle ein paar Anmerkungen zur Schreibweise: Schreibt man z. B. ''AC'', so wird damit eine Gerade bezeichnet, die durch die beiden Punkte ''A'' und ''C'' verläuft. Die Strecke <math>\overline{AC}</math> kennzeichnen wir mit einem Strich oben drauf. Möchten Sie die Aussage treffen, dass die beiden Strecken <math>\overline{AC}</math> und <math>\overline{BC}</math> gleichlang sind, können Sie das folgendermaßen machen: <math>\overline{AC}\tilde {=}\overline{BC} </math> oder <math>\left| AC \right|=\left| BC \right|</math>. (Das können Sie jetzt noch nicht wissen, da wir das noch nicht behandelt haben, aber ich möchte nur vermeiden, dass sich was Falsches einprägt)--[[Benutzer:Schnirch|Schnirch]] 14:24, 10. Nov. 2011 (CET) | ||
Aktuelle Version vom 10. November 2011, 14:24 Uhr
Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
a) Wie lautet die Umkehrung des Basiswinkelsatzes?
b) Fassen Sie den Basiswinkelsatz und seine Umkehrung zu einem Satz zusammen (Kriterium).
a) Ein Dreieck, dessen Basiswinkel kongruent zueinander sind, ist ein gleichschenkliges Dreieck. b) Genau dann,wenn die Basiswinkel eines Dreieckes kongruent zueinander sind, ist das Dreieck gleichschenklig.--Miriam 12:35, 4. Nov. 2011 (CET)
@ Miriam: Ich würde statt Basiswinkel eher Innenwinkel verwenden. a) Wenn in einem Dreieck zwei beliebige Innenwinkel kongruent zueinander sind, dann ist das Dreieck gleichschenklig. b) Genau dann, wenn in einem Dreieck zwei beliebige Innenwinkel kongruent zueinander sind, ist das Dreieck gleichschenklig. --Todah raba 18:24, 4. Nov. 2011 (CET)
Satz:
Sei ABC ein Dreieck, für das gilt, die Strecke AC ist kongruent zur Strecke BC, dann gilt Winkel BAC ist kongruent zum Winkel ABC.
Wozu steht dieser Satz hier? Zu welcher (Teil)aufgabe gehört er? --Tutorin Anne 15:16, 8. Nov. 2011 (CET)
Und, wer hat den Satz hier reingestellt? Bitte immer die Signatur mit angeben, damit jeder Leser zwischen Aufgaben, Skript und studentischen Beiträgen unterscheiden kann, danke!--Schnirch 14:11, 10. Nov. 2011 (CET)
AC = BC «» Winkel BAC = Winkel ABC (Aquivalenz, wenn Aussage rechts wahr ist, ist auch Aussage links wahr und umgekehrt.)--Costa rica 15:25, 7. Nov. 2011 (CET)
An dieser Stelle ein paar Anmerkungen zur Schreibweise: Schreibt man z. B. AC, so wird damit eine Gerade bezeichnet, die durch die beiden Punkte A und C verläuft. Die Strecke 
kennzeichnen wir mit einem Strich oben drauf. Möchten Sie die Aussage treffen, dass die beiden Strecken und 
gleichlang sind, können Sie das folgendermaßen machen: 
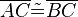oder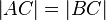 
. (Das können Sie jetzt noch nicht wissen, da wir das noch nicht behandelt haben, aber ich möchte nur vermeiden, dass sich was Falsches einprägt)--Schnirch 14:24, 10. Nov. 2011 (CET)
