Übung vom 13.01.12: Unterschied zwischen den Versionen
Adores (Diskussion | Beiträge) |
Adores (Diskussion | Beiträge) |
||
| Zeile 39: | Zeile 39: | ||
[[Datei:6Aufgabe 3.1.jpg|400px]]<br /> | [[Datei:6Aufgabe 3.1.jpg|400px]]<br /> | ||
<br /> | <br /> | ||
| − | --> Achtung:Der Beweis ist korrekt, es ist aber nicht zu empfehlen, den Beweis in der Prüfung so zu formulieren( aus Zeit- und Platzgründen). | + | --> Achtung:Der Beweis ist korrekt, es ist aber nicht zu empfehlen, den Beweis in der Prüfung so zu formulieren( aus Zeit- und Platzgründen).<br /> |
| + | <br /> | ||
<br /> | <br /> | ||
==Beweis 3== | ==Beweis 3== | ||
[[Datei:6Aufgabe 3.2.jpg|400px]]<br /> | [[Datei:6Aufgabe 3.2.jpg|400px]]<br /> | ||
<br /> | <br /> | ||
| − | --[[Benutzer:Adores|Adores]] 18: | + | --[[Benutzer:Adores|Adores]] 18:44, 13. Jan. 2012 (CET) |
Aktuelle Version vom 13. Januar 2012, 18:44 Uhr
Hier findet ihr alle Aufgaben und Lösungen/Lösungsversuche:
Inhaltsverzeichnis |
Aufgabe 1: Definieren Sie den Begriff Halbkreis
Definition 1
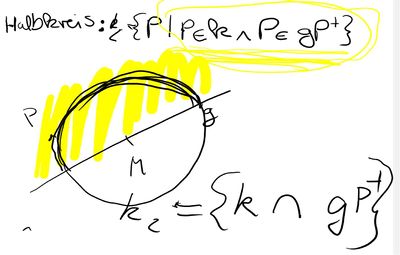
-->Die gelb umkreiste Definition könnte man auch kürzer schreiben, dennoch ist sie korrekt.
Definition 2
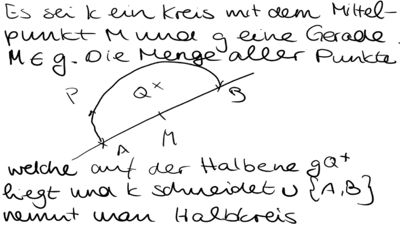
--> Achtung: Definition nicht komplett richtig, die Punkte A und B gehören bereits zur Menge, da sie zur Trägergeraden der Halbebene gehören. Sie müssen nicht mehr vereinigt werden.
Definition 3
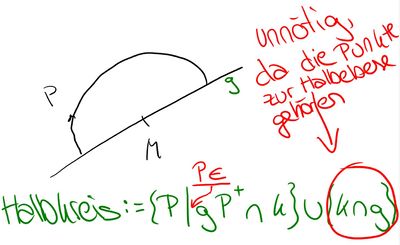
--> Achtung: Zwei bereits verbesserte Probleme, entweder muss man das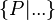 
weglassen oder eben 
.
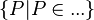Aufgabe 2: Heranführung an den Satz des Thales.
Heranführung 1
Heranführung 2
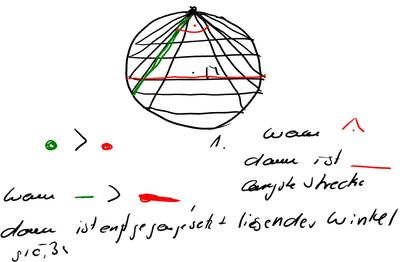
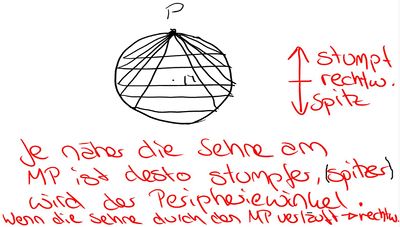
--> Achtung: Hier lässt sich durch die Seite keine Aussage über den Winkel fällen. Größte mögliche Seite, wäre der Durchmesser, wird die Seite in Richtung des Peripheriewinkels verschoben, so wird der Winkel größer, was eien Widerspruch zur Aussage darstellt.
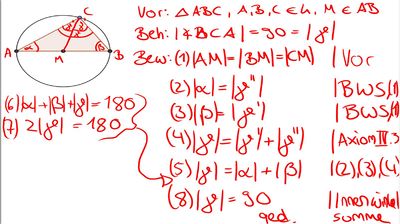
Aufgabe 3: Beweis: Satz des Thales.
Beweis 1
Beweis 2
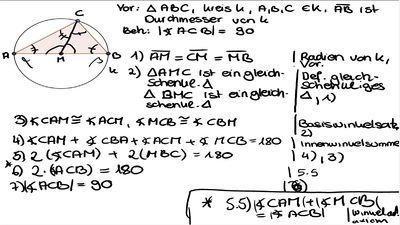
--> Achtung:Der Beweis ist korrekt, es ist aber nicht zu empfehlen, den Beweis in der Prüfung so zu formulieren( aus Zeit- und Platzgründen).
Beweis 3
--Adores 18:44, 13. Jan. 2012 (CET)
