Köln-Triangle: Unterschied zwischen den Versionen
HecklF (Diskussion | Beiträge) |
|||
| Zeile 19: | Zeile 19: | ||
<br />Kann jemand mal seine Idee hier einstellen, ich komm mit der Volumenberechnung einfach nicht weiter. Danke!--[[Benutzer:Löwenzahn|Löwenzahn]] 18:06, 21. Jan. 2012 (CET)<br /><br /><br /> | <br />Kann jemand mal seine Idee hier einstellen, ich komm mit der Volumenberechnung einfach nicht weiter. Danke!--[[Benutzer:Löwenzahn|Löwenzahn]] 18:06, 21. Jan. 2012 (CET)<br /><br /><br /> | ||
| + | ==== Lösungsvorschlag 1 ==== | ||
Hallo Löwenzahn! Hier meine Lösung - wäre super, wenn du die Lösungsidee kommentierten könntest, da ich sie bisher noch nicht mit anderen Lösungswegen verglichen habe. | Hallo Löwenzahn! Hier meine Lösung - wäre super, wenn du die Lösungsidee kommentierten könntest, da ich sie bisher noch nicht mit anderen Lösungswegen verglichen habe. | ||
<br /><br /> | <br /><br /> | ||
a)<br /> | a)<br /> | ||
| − | h: Höhe des Turms: ~70m (Stützpunktvorstellung: 20 Stockwerke á je 3,5m)<br /> | + | h: Höhe des Turms: ~70m (Stützpunktvorstellung: 20 Stockwerke á je 3,5m)<br />Ausrechnen vo |
b: Länge Kreisbogen: ~38m (Stützpunktvorstellung: 25 Fenster pro Kriesbogen á je 1,5m)<br /><br /> | b: Länge Kreisbogen: ~38m (Stützpunktvorstellung: 25 Fenster pro Kriesbogen á je 1,5m)<br /><br /> | ||
mathematisches Modell:<br /> | mathematisches Modell:<br /> | ||
| Zeile 38: | Zeile 39: | ||
--> s=0,513 [dm]<br /> | --> s=0,513 [dm]<br /> | ||
--> h=1,075dm=10,7cm , s=5,13cm , b=5,37cm<br /><br />--[[Benutzer:Libertad|Libertad]] 19:08, 22. Jan. 2012 (CET) | --> h=1,075dm=10,7cm , s=5,13cm , b=5,37cm<br /><br />--[[Benutzer:Libertad|Libertad]] 19:08, 22. Jan. 2012 (CET) | ||
| − | |||
| − | |||
|} | |} | ||
| + | <br /><br />'''Kommentar'''<br /> | ||
| + | Hallo Libertad, vielen Dank, dass du deine Lösung eingestellt hast. Ich habe ähnlich gerechnet wie du, und auch für a) ähnliche Ergebnisse raus.<br /> | ||
| + | Ich habe angenommen:<br /> | ||
| + | Höhe: 20 Stockwerke à 4m = 80 m<br /> | ||
| + | Kreisbogen: 20 Fenster à 1,5m = 30 m<br /> | ||
| + | Für das Volumen des Reuleaux-Dreiecks habe ich dann gerundet 47360 m³. Allerdings habe ich dann das Problem bei der Umrechnung in Hektoliter. Ich habe folgendes: 47360 m³ = 47.360.000L = 473.600 hL (du hast eine Nullstelle mehr?!) | ||
| + | Gerechnet habe ich wesentlich kleinschrittiger, letztendlich hatte ich aber dann die gleiche Formel. Die Aufgabe b) muss ich nochmal anschauen, bevor ich antworten kann. Gruß --[[Benutzer:Löwenzahn|Löwenzahn]] 15:08, 23. Jan. 2012 (CET)<br /> | ||
Version vom 23. Januar 2012, 15:08 Uhr
Die oberen 20 Stockwerke und die Aussichtsplattform des KölnTriangles haben als Grundriss ein Reuleaux Dreieck:
Es sei  ein gleichseitiges Dreieck mit der Seitenlänge s.
ein gleichseitiges Dreieck mit der Seitenlänge s.
Unter 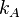 ;
; 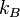 und
und 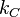 wollen wir die Kreise mit den Mittelpunkten
wollen wir die Kreise mit den Mittelpunkten 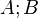 und
und und dem Radius
und dem Radius  verstehen.
verstehen.
Das Reuleaux Dreiecks mit den Eckpunkten 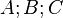 ist die Vereinigungsmenge der drei Kreisbögen
ist die Vereinigungsmenge der drei Kreisbögen  ;
;  und
und  , wobei
, wobei  der kürzere Bögen des Kreises
der kürzere Bögen des Kreises 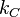 zwischen den Punkten
zwischen den Punkten  und
und  ist.
ist.
Analog sind die Bögen  und
und  auf den Kreisen
auf den Kreisen 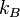 bzw.
bzw. 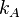 zu verstehen.
zu verstehen.
Die Dom-Brauerei möchte eine neue Kölschsorte kreieren. Die beauftagte Werbefirma macht den Vorschlag, das neue Bier Triangle-Kölsch zu nennen und das äußere Design des neuen Biers mit dem KölnTriangle zu verbinden.
a)Die Werbefachleute stellen sich vor, dass der auf Abbildung 1 (Wikipedia) sichtbare Teil des KölnTriangles eine Dose in Form eines Reuleaux-Dreieck-Zylinders ist.
Welche Menge Triangle-Kölsch würden in diese Dose passen? Die Länge bs der Kreisbögen des Releaux Dreiecks und die Höhe h dieser Dose könnte man
abschätzen. Entwickeln Sie eine Formel zur Berechnung des Volumens eines Reuleaux-Dreiecks-Zylinders, in die nur bs und h als zu messende bzw. abzuschätzende Größen eingehen.
Schätzen Sie bs und h auf der Grundlage von Abbildung 1 und berechnen Sie das Volumen des entsprechenden Reuleaux-Dreiecks-Zylinders in Hektolitern.
b) Kölsch wird üblicherweise in Mengen von 0,2 Litern verabreicht. Das neue Bier soll in Dosen verkauft werden, die dem Reuleaux-Dreieck-Zylinder aus Aufgabe a) (mathematisch) ähnlich sind. Gehen Sie davon aus, dass das von Ihnen berechnete Volumen in Hektolitern aus Aufgabe a) korrekt ist und berechnen Sie auf dieser Grundlage die Maße der entsprechenden 0,2 Liter Dose.
Verständnisfrage: Die Seitenlänge des gleichseitigen Dreiecks und die Höhe des gleichseitigen Dreiecks können aber aus den zu messenden bzw. abzuschätzenden Angaben errechnet werden und zur Volumenberechnung genutzt werden oder? --Libertad 18:50, 3. Jan. 2012 (CET)
Kann jemand mal seine Idee hier einstellen, ich komm mit der Volumenberechnung einfach nicht weiter. Danke!--Löwenzahn 18:06, 21. Jan. 2012 (CET)
Lösungsvorschlag 1
Hallo Löwenzahn! Hier meine Lösung - wäre super, wenn du die Lösungsidee kommentierten könntest, da ich sie bisher noch nicht mit anderen Lösungswegen verglichen habe.
a)
h: Höhe des Turms: ~70m (Stützpunktvorstellung: 20 Stockwerke á je 3,5m)
Ausrechnen vo
b: Länge Kreisbogen: ~38m (Stützpunktvorstellung: 25 Fenster pro Kriesbogen á je 1,5m)
mathematisches Modell:
V= (3*pi*s²*60/360*h)-(2*s²/4*Wurzel3*h)
Fehlende Größe: Seitenlänge s bzw. Radius s:
b=2*pi*s*alpha/360
--> 38=2*pi*s*60/360 --> s=33,41 [m]
V=(3*pi*33,41²*60/360*70)-(2*33,41²/4* wurzel 3 *70) = 55067,96 m³ was 5.506.796 hl entspricht
b)
Idee: Höhe des Zylinders in Abhängigkeit von s angeben:
h=70m=700dm
s=33,41m=334,1dm
h=700/334,1 * s
in Formel einsetzen (V=0,2 dm³):
0,2 = (3*pi*s²*60/360*700/334,1*s)-(2*s²/4* Wurzel 3*7000/3341*s)
--> s=0,513 [dm]
--> h=1,075dm=10,7cm , s=5,13cm , b=5,37cm
--Libertad 19:08, 22. Jan. 2012 (CET)
|}
Kommentar
Hallo Libertad, vielen Dank, dass du deine Lösung eingestellt hast. Ich habe ähnlich gerechnet wie du, und auch für a) ähnliche Ergebnisse raus.
Ich habe angenommen:
Höhe: 20 Stockwerke à 4m = 80 m
Kreisbogen: 20 Fenster à 1,5m = 30 m
Für das Volumen des Reuleaux-Dreiecks habe ich dann gerundet 47360 m³. Allerdings habe ich dann das Problem bei der Umrechnung in Hektoliter. Ich habe folgendes: 47360 m³ = 47.360.000L = 473.600 hL (du hast eine Nullstelle mehr?!)
Gerechnet habe ich wesentlich kleinschrittiger, letztendlich hatte ich aber dann die gleiche Formel. Die Aufgabe b) muss ich nochmal anschauen, bevor ich antworten kann. Gruß --Löwenzahn 15:08, 23. Jan. 2012 (CET)

