Lösung von Aufg. 13.7 (WS 11/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Adores (Diskussion | Beiträge) |
|||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie: Ein Punkt <math>\ P</math> gehört genau dann zur Winkelhalbierenden des Winkels <math>\ \alpha</math>, wenn er zu den Schenkeln von <math>\ \alpha</math> jeweils denselben Abstand hat. | Beweisen Sie: Ein Punkt <math>\ P</math> gehört genau dann zur Winkelhalbierenden des Winkels <math>\ \alpha</math>, wenn er zu den Schenkeln von <math>\ \alpha</math> jeweils denselben Abstand hat. | ||
* Dürfen wir SsW benutzen?--[[Benutzer:Miriam|Miriam]] 12:13, 21. Jan. 2012 (CET) | * Dürfen wir SsW benutzen?--[[Benutzer:Miriam|Miriam]] 12:13, 21. Jan. 2012 (CET) | ||
| − | ** Ja, du kannst SsW benutzen. Allerdings musst du dann immer begründen, dass S (lange Seite) wirklich länger als s (kurze Seite) ist. Das ist meist schwer zu zeigen.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 13:06, 25. Jan. 2012 (CET)<br /> | + | ** Ja, du kannst SsW benutzen. Allerdings musst du dann immer begründen, dass S (lange Seite) wirklich länger als s (kurze Seite) ist. Das ist meist schwer zu zeigen.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 13:06, 25. Jan. 2012 (CET) Wobei das hier mit dem 90° Winkel ganz gut begründet werden kann. Dem 90° liegt immer die längst Seite entgegen. --[[Benutzer:Tutorin Anne|Tutorin Anne]] 17:06, 29. Jan. 2012 (CET)<br /> |
| − | * Wenn man für die Rückrichtung "<-" gezeigt hat, dass <math>\alpha1 \tilde {=} \alpha2</math>, also die beiden Winkel, die durch die Winkelhalbierende erzeugt wurden, muss man dann zusätzlich noch zeigen, dass P im Inneren des Winkels liegt? --[[Benutzer:Todah raba|Todah raba]] 19:29, 25. Jan. 2012 (CET)<br /><br /> | + | * Wenn man für die Rückrichtung "<-" gezeigt hat, dass <math>\alpha1 \tilde {=} \alpha2</math>, also die beiden Winkel, die durch die Winkelhalbierende erzeugt wurden, muss man dann zusätzlich noch zeigen, dass P im Inneren des Winkels liegt? --[[Benutzer:Todah raba|Todah raba]] 19:29, 25. Jan. 2012 (CET) |
| − | + | ** Ja, so steht's ja in der Definition.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 17:06, 29. Jan. 2012 (CET) | |
| + | <br /><br /> | ||
HILFE!!! Sind wir beim Winkelhalbierendenkriterium in der Euklidischen Geometrie oder in der Absoluten? | HILFE!!! Sind wir beim Winkelhalbierendenkriterium in der Euklidischen Geometrie oder in der Absoluten? | ||
| − | Dies ist ein echtes Problem, da es für mich eindeutig zur absoluten Geometrie gehört, ich aber die Rückrichtung nicht Ohne Innenwinkelsumme lösen kann.--[[Benutzer:Adores|Adores]] 00:27, 26. Jan. 2012 (CET) | + | Dies ist ein echtes Problem, da es für mich eindeutig zur absoluten Geometrie gehört, ich aber die Rückrichtung nicht Ohne Innenwinkelsumme lösen kann.--[[Benutzer:Adores|Adores]] 00:27, 26. Jan. 2012 (CET)<br /><br /> |
| − | + | Mh, ich glaube, ich verstehe, dass du die Innenwinkelsumme nutzt. Du hast 2 kongruente Winkel und eine Seite in der Anordung WWS und möchtest dann denn Kongruenzsatz WSW anwenden. Also berechnest du den dritten Innenwinkel. Oder? Ich weiß auch nicht, in welche Geometrie dieser Beweis gehört. Falls er wirklich zur absoluten Geomtrie gehört, dann kann man den Kongruenzsatz WWS wohl auch ohne Parallelenaxiom aus dem Satz WSW herleiten. Das wäre die einzige Erklärung, die mir so einfällt.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 17:06, 29. Jan. 2012 (CET) | |
| − | + | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 29. Januar 2012, 17:06 Uhr
Beweisen Sie: Ein Punkt 
gehört genau dann zur Winkelhalbierenden des Winkels 
, wenn er zu den Schenkeln von jeweils denselben Abstand hat.
- Dürfen wir SsW benutzen?--Miriam 12:13, 21. Jan. 2012 (CET)
- Ja, du kannst SsW benutzen. Allerdings musst du dann immer begründen, dass S (lange Seite) wirklich länger als s (kurze Seite) ist. Das ist meist schwer zu zeigen.--Tutorin Anne 13:06, 25. Jan. 2012 (CET) Wobei das hier mit dem 90° Winkel ganz gut begründet werden kann. Dem 90° liegt immer die längst Seite entgegen. --Tutorin Anne 17:06, 29. Jan. 2012 (CET)
- Ja, du kannst SsW benutzen. Allerdings musst du dann immer begründen, dass S (lange Seite) wirklich länger als s (kurze Seite) ist. Das ist meist schwer zu zeigen.--Tutorin Anne 13:06, 25. Jan. 2012 (CET) Wobei das hier mit dem 90° Winkel ganz gut begründet werden kann. Dem 90° liegt immer die längst Seite entgegen. --Tutorin Anne 17:06, 29. Jan. 2012 (CET)
- Wenn man für die Rückrichtung "<-" gezeigt hat, dass
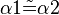, also die beiden Winkel, die durch die Winkelhalbierende erzeugt wurden, muss man dann zusätzlich noch zeigen, dass P im Inneren des Winkels liegt? --Todah raba 19:29, 25. Jan. 2012 (CET)
- Ja, so steht's ja in der Definition.--Tutorin Anne 17:06, 29. Jan. 2012 (CET)
HILFE!!! Sind wir beim Winkelhalbierendenkriterium in der Euklidischen Geometrie oder in der Absoluten?
Dies ist ein echtes Problem, da es für mich eindeutig zur absoluten Geometrie gehört, ich aber die Rückrichtung nicht Ohne Innenwinkelsumme lösen kann.--Adores 00:27, 26. Jan. 2012 (CET)
Mh, ich glaube, ich verstehe, dass du die Innenwinkelsumme nutzt. Du hast 2 kongruente Winkel und eine Seite in der Anordung WWS und möchtest dann denn Kongruenzsatz WSW anwenden. Also berechnest du den dritten Innenwinkel. Oder? Ich weiß auch nicht, in welche Geometrie dieser Beweis gehört. Falls er wirklich zur absoluten Geomtrie gehört, dann kann man den Kongruenzsatz WWS wohl auch ohne Parallelenaxiom aus dem Satz WSW herleiten. Das wäre die einzige Erklärung, die mir so einfällt.--Tutorin Anne 17:06, 29. Jan. 2012 (CET)
