Lösung von Aufgabe 6.9: Unterschied zwischen den Versionen

Version vom 24. Mai 2010, 11:54 Uhr

Satz:

Von drei Punkten $\ A, B$ und $\ C$ ein und derselben Geraden $\ g$ liegt genau einer zwischen den beiden anderen.

Beweisen Sie diesen Satz.
Satz in wenn-dann:

Wenn drei Punkte $\ A, B$ und $\ C$ ..., dann ... .

Beweis

Es seien also $\ A, B$ und $\ C$ drei Punkte.
Voraussetzung:

...

Behauptung

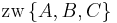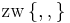$\operatorname{zw}\left \{A, B, C \right \}$ oder $\operatorname{zw}\left \{ , , \right \}$ oder $\operatorname{zw}\left \{ , , \right \}$

@@ Zeile 8: / Zeile 8: @@
 Es seien also <math>\ A, B</math> und <math>\ C</math> drei Punkte.<br />
-<u>'''Voraussetzung:'''</u><br />
+<u>'''Voraussetzung:'''</u>
-...<br />
+...
 <u>'''Behauptung'''</u><br />
 ::<math>\operatorname{zw}\left \{A, B, C \right \}</math> oder <math>\operatorname{zw}\left \{ ,  ,   \right \}</math> oder <math>\operatorname{zw}\left \{ ,  ,  \right \}</math>