Lösung von Aufgabe 3.2 S (SoSe 12): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Bemerkung von M.G. zu c) |
*m.g.* (Diskussion | Beiträge) (→Lösungsvorschlag 3 von Mahe84) |
||
| Zeile 51: | Zeile 51: | ||
Wenn ein Viereck ein Parallelogramm ist, dann sind die gegenüberliegenden Seiten parallel und gleich lang. | Wenn ein Viereck ein Parallelogramm ist, dann sind die gegenüberliegenden Seiten parallel und gleich lang. | ||
Wenn die gegenüberliegenden Seiten in einem Viereck parallel und gleich lang sind, so ist es ein Parallelogramm. --[[Benutzer:Mahe84|Mahe84]] 12:11, 8. Mai 2012 (CEST) | Wenn die gegenüberliegenden Seiten in einem Viereck parallel und gleich lang sind, so ist es ein Parallelogramm. --[[Benutzer:Mahe84|Mahe84]] 12:11, 8. Mai 2012 (CEST) | ||
| + | ====Kommentar M.G. zu Lösungsvorschlag 3==== | ||
| + | @Mahe84 | ||
| + | Man kann natürlich den Begriff Parallelogramm über die Parallelität der Seiten definieren. Wir man in der Schule auch tun, denn schließlich wird man damit der Semantik der Begriffsbezeichnung gerecht. In unserer Aufgabe versuchen wir jedoch zu einer anderen Definition für den Begriff des Parallelogramms zu kommen. Das Halbieren der Diagonalen könnte hilfreich dabei sein. | ||
| + | |||
| + | Sie haben richtig erkannt, dass definierende Eigenschaften Kriterien sein müssen. Klar, sonst könnte man ja nicht den Begriff eindeutig festlegen. Mit eine "Definition" wie ein Quadrat ist ein Viereck mit der parallelen Seiten erwischt man natürlich die Quadrate aber nicht nur die. | ||
| + | |||
| + | Definitionen könnte und kann man natürlich in Genau-Dann-Wenn Form schreiben. Muss man aber nicht, da bei einer Definition immer klar ist, dass die definierende Eigenschaft ein Kriterium ist. Zwei Implikationen (Implikation und ihre Umkehrung) gehen aber nicht als Definition durch. Sie könnten eher schreiben Ein Viereck heißt genau dann Parallelogramm, wenn seine gegenüberliegenden Seiten parallel sind. (Ich glaub das reicht oder? Oder könnte es ein Viereck geben, in dem zwar die gegenüberliegenden seiten parallel aber nicht gleichlang sind?) | ||
| + | Der Mathematiker schreibt das dann mitunter auch so: | ||
| + | {{Definition|Parallelogramm<br />Ein Viereck heißt Parallelogramm<math>:\Longleftrightarrow</math> Die gegenüberliegenden Seiten des Vierecks sind parallel.}} | ||
Version vom 8. Mai 2012, 21:45 Uhr
Inhaltsverzeichnis |
Aufgabe 3.2
a)Ergänzen Sie so, dass sowohl die Hin- als auch die Rückrichtung wahr sind:
Wenn ein Viereck ein/e ... ist, halbieren sich seine Diagonalen.
Wenn sich die Diagonalen eines Vierecks halbieren, so ist es ein/e ....
b)Formulieren sie eine Äquivalenz.
c)Definieren Sie die Vierecksart durch das gefundene Kriterium.
Lösungsvorschlag 1:
a)
Wenn ein Viereck  ein Parallelogramm ist, halbieren sich seine Diagonalen.
ein Parallelogramm ist, halbieren sich seine Diagonalen.
Wenn sich die Diagonalen eines Vierecks  halbieren, so ist es ein Parallelogramm.
halbieren, so ist es ein Parallelogramm.
b) Genau dann wenn sich die Diagonalen eines Vierecks  halbieren, ist es ein Parallelogramm.
halbieren, ist es ein Parallelogramm.
c) Ein Viereck  , dessen Diagonalen sich gegenseitig halbieren, ist ein Parallelogramm. --Goliath 15:38, 3. Mai 2012 (CEST) <be/>
, dessen Diagonalen sich gegenseitig halbieren, ist ein Parallelogramm. --Goliath 15:38, 3. Mai 2012 (CEST) <be/>
Coole Sache. Wenn man sagt Parallelogramm, dann schließt das ja nicht aus, dass es auch ein Quadrat oder eine Raute oder so ist.--RitterSport 20:46, 6. Mai 2012 (CEST)
Lösungsvorschlag 2:
a)
A: Viereck Parallelogramm
B: Diagonalen halbieren sich
Viereck Parallelogramm  Diagonalen halbieren sich also A
Diagonalen halbieren sich also A  B
B
Diagonalen halbieren sich  Viereck Parallelogramm also B
Viereck Parallelogramm also B  A
A
b) A  B
B
c) Wie ist die Kurzschreibweise hierfür? --Hauleri 13:26, 6. Mai 2012 (CEST)
Ich weiß es nicht genau. Ich denke man muss schreiben: "Sich halbierende Diagonalen sind ein Kriterium für ein Parallelogramm"--RitterSport 20:49, 6. Mai 2012 (CEST)
Bemerkung von M.G. zu c
Begriffe definiert man über die Eigenschaften ihrer Repräsentanten. So hat z.B. jedes spezielle Quadrat die Eigenschaft, 4 Symmetrieachsen zu besitzen. Da diese Eigenschaft notwendig und hinreichend dafür ist, dass ein Viereck ein Quadrat ist, könnte man die Eigenschaft vier Symmetrieachsen zu haben auch als definierende Eigenschaft verwenden.
Definition
Quadrat
Ein Viereck mit vier Symmetrieachsen heißt Quadrat.
Wie sieht es nun mit der Eigenschaft von Vierecken aus, einander halbierende Diagonalen zu haben? Ist das eine notwendige und hinreichende Bedingung, dass unser Viereck ein Parallelogramm ist? Oder anders ist die Menge der Vierecke mit einander halbierenden Diagonalen identisch zur Menge der Parallelogramme nach üblicher Definition über die Parallelität von Seiten? Also gesucht ist eine mögliche andere Definition des Begriffs Parallelogramm.--*m.g.* 13:02, 7. Mai 2012 (CEST)
Lösungsvorschlag 3 von Mahe84
Wenn ein Viereck ein Parallelogramm ist, dann sind die gegenüberliegenden Seiten parallel und gleich lang. Wenn die gegenüberliegenden Seiten in einem Viereck parallel und gleich lang sind, so ist es ein Parallelogramm. --Mahe84 12:11, 8. Mai 2012 (CEST)
Kommentar M.G. zu Lösungsvorschlag 3
@Mahe84 Man kann natürlich den Begriff Parallelogramm über die Parallelität der Seiten definieren. Wir man in der Schule auch tun, denn schließlich wird man damit der Semantik der Begriffsbezeichnung gerecht. In unserer Aufgabe versuchen wir jedoch zu einer anderen Definition für den Begriff des Parallelogramms zu kommen. Das Halbieren der Diagonalen könnte hilfreich dabei sein.
Sie haben richtig erkannt, dass definierende Eigenschaften Kriterien sein müssen. Klar, sonst könnte man ja nicht den Begriff eindeutig festlegen. Mit eine "Definition" wie ein Quadrat ist ein Viereck mit der parallelen Seiten erwischt man natürlich die Quadrate aber nicht nur die.
Definitionen könnte und kann man natürlich in Genau-Dann-Wenn Form schreiben. Muss man aber nicht, da bei einer Definition immer klar ist, dass die definierende Eigenschaft ein Kriterium ist. Zwei Implikationen (Implikation und ihre Umkehrung) gehen aber nicht als Definition durch. Sie könnten eher schreiben Ein Viereck heißt genau dann Parallelogramm, wenn seine gegenüberliegenden Seiten parallel sind. (Ich glaub das reicht oder? Oder könnte es ein Viereck geben, in dem zwar die gegenüberliegenden seiten parallel aber nicht gleichlang sind?) Der Mathematiker schreibt das dann mitunter auch so:
Definition
Parallelogramm
Ein Viereck heißt Parallelogramm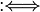 Die gegenüberliegenden Seiten des Vierecks sind parallel.
Die gegenüberliegenden Seiten des Vierecks sind parallel.

