Lösung von Aufgabe 4.2P (SoSe 12): Unterschied zwischen den Versionen
| Zeile 19: | Zeile 19: | ||
Frage vorweg: Müssen wir nur den ersten Teil (gSh) auf seine Eigenschaften untersuchen, oder die ganze Äquivalenz?; in der Aufgabe steht nämlich nur "Relation S". | Frage vorweg: Müssen wir nur den ersten Teil (gSh) auf seine Eigenschaften untersuchen, oder die ganze Äquivalenz?; in der Aufgabe steht nämlich nur "Relation S". | ||
| − | + | Ich habe gerade ein totales Wirrwarr im Kopf. | |
| − | + | Reflexiv: Zum einen kann man sagen, dass g sich nicht selbst schneiden kann (Relationszeichen S), aber man kann sagen, dass die Schnittmenge von identischen Punktmengen (g schneidet g)(und Geraden sind ja nichts anderes als Punktmengen) die selben Elemente enthält und nie leer sein kann! | |
| + | Symmetrisch: Wenn gSh, dann gilt auch hSg (kommutativ) | ||
| + | Transitiv: | ||
| + | gSh und hSi, dann gSi | ||
| + | In fast immer falsch, außer wenn g=i. --[[Benutzer:Honeydukes|Honeydukes]] 19:18, 12. Mai 2012 (CEST) | ||
| + | |||
| + | |||
| + | |||
[[Category:Einführung_P]] | [[Category:Einführung_P]] | ||
Version vom 12. Mai 2012, 18:18 Uhr
Untersuchen Sie folgende Relation S auf ihre Eigenschaften:
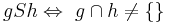
Reflexiv, symmetrisch und transitiv 
Äquivalenzrelation --Malilglowka 17:29, 10. Mai 2012 (CEST)
reflexiv: würde ich zustimmen, denn eine menge mit sich selbst geschnitten keine leere menge ergibt
symmetrisch: ja, weil das kommutativgesetz gilt (auch g und h haben keine leere menge.
transitiv: würde ich dir nicht zustimmen: wenn g geschnitten mit h keine leere menge hat und h mit i geschnitten keine leere menge, können wir nichts darüber aussagen, ob g und i geschnitten nicht doch eine leere menge haben
- zahlenbeispiel: wenn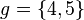 
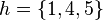und 
und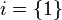 
, dann haben g geschnitten mit i eine leere menge.
- beispiel aus der geometrie: wenn g eine gerade ist und h schneidet g, dann hätte i, wenn sie zu g parallel ist, zwar auch einen punkt mit h gemeinsam, aber nicht zur parallelen geraden g--Studentin 19:21, 10. Mai 2012 (CEST)
transitiv : gRh und hRc 
gRc
somit gRh stimmt ja somit ist die Aussage wahr und hRc geht nicht, da kein c definiert ist, somit ist hRc falsch. Alles in allem ist die wahre Aussage und falsche Aussage immer eine falsche Aussage (UND-Aussage). Und durch die Implikation ist es egal was hinten raus kommt die Aussage ist wahr ( Aussage). Hoffe konnte es verständlich ausführen.--Malilglowka 23:41, 10. Mai 2012 (CEST)
ich verstehe , was du meinst. aber sind wir nicht immer von einem unbekannten dritten ausgegangen und haben wir damit überprüft, ob etwas transitiv ist oder nicht?--Studentin 00:15, 11. Mai 2012 (CEST)
Frage vorweg: Müssen wir nur den ersten Teil (gSh) auf seine Eigenschaften untersuchen, oder die ganze Äquivalenz?; in der Aufgabe steht nämlich nur "Relation S".
Ich habe gerade ein totales Wirrwarr im Kopf. Reflexiv: Zum einen kann man sagen, dass g sich nicht selbst schneiden kann (Relationszeichen S), aber man kann sagen, dass die Schnittmenge von identischen Punktmengen (g schneidet g)(und Geraden sind ja nichts anderes als Punktmengen) die selben Elemente enthält und nie leer sein kann! Symmetrisch: Wenn gSh, dann gilt auch hSg (kommutativ) Transitiv: gSh und hSi, dann gSi In fast immer falsch, außer wenn g=i. --Honeydukes 19:18, 12. Mai 2012 (CEST)
