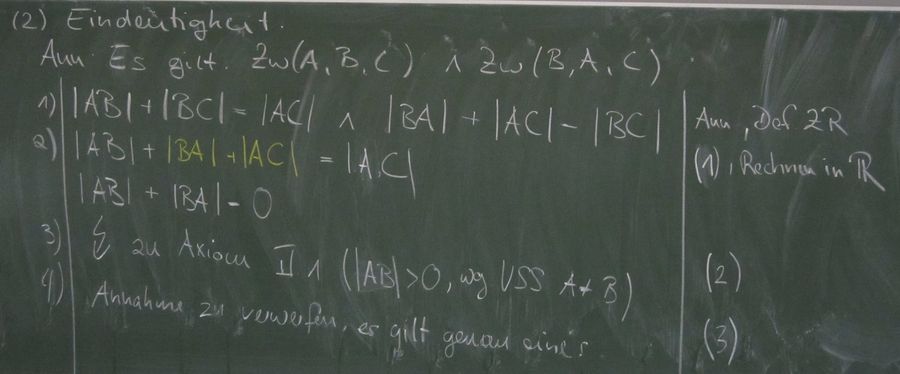Lösungsideen Übung Heckl 23.05.2012: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 5.3)
(→‎Platz für Kommentare zu Aufgabe 5.2)
Zeile 39: Zeile 39:
  
 
<br />
 
<br />
 +
== Aufgabe 5.5 ==
 +
Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 4.3 und Zusatzaufgabe 4.4).<br /><br />
 +
===Ein bereitgestelltes Skript einer Übungsteilnehmerin - dankeschön===
 +
[[Datei: 5_5_s_1.JPG | 900px]]
 +
<br /><br />
 +
[[Datei: 5_5_s_2.JPG | 900px]]
 +
<br /><br />
 +
 +
===Aus der Übung===
 +
[[Datei: 23052012_5_5.JPG | 900px]]
 +
<br /><br /><br />
 +
[[Datei: 23052012_5_5_z.JPG | 900px]]
 +
<br />--[[Benutzer:HecklF|Flo60]] 21:45, 23. Mai 2012 (CEST)
 +
 +
===Platz für Kommentare zu Aufgabe 5.5===
 +
<br />
 +
 +
 +
 +
 +
<br />
 +
 +
=Zurück zur Übungsseite=
 +
[[Übung Aufgaben 5 S (SoSe 12)]]
 +
 +
[[Kategorie: Einführung_S]] [[Kategorie: WIKI-Übung-Heckl]]

Version vom 23. Mai 2012, 20:45 Uhr

Inhaltsverzeichnis

Aufgabe 5.1

Satz:

Von drei paarweise verschiedenen Punkten \ A, B und \ C ein und derselben Geraden \ g liegt genau einer zwischen den beiden anderen.



23052012 5 1 1.JPG 

Die Behauptung wurde auf zwei verschiedene Arten und Weisen formuliert!



23052012 5 1 2.JPG 

Diese gelben 'Häckchen' sind in Wirklichkeit keine 'Häckchen', sondern bedeuten das aussagelogische ODER (\vee)



23052012 5 1 3.JPG
--Flo60 21:29, 23. Mai 2012 (CEST)

Platz für Kommentare zu Aufgabe 5.1




Aufgabe 5.3

Zeigen Sie, dass für drei paarweise verschiedene Punkte \ A, B und \ C gilt:
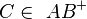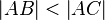Wenn C \in \ AB^{+} und \left| AB \right| < \left| AC \right| dann gilt \operatorname Zw (A, B, C)

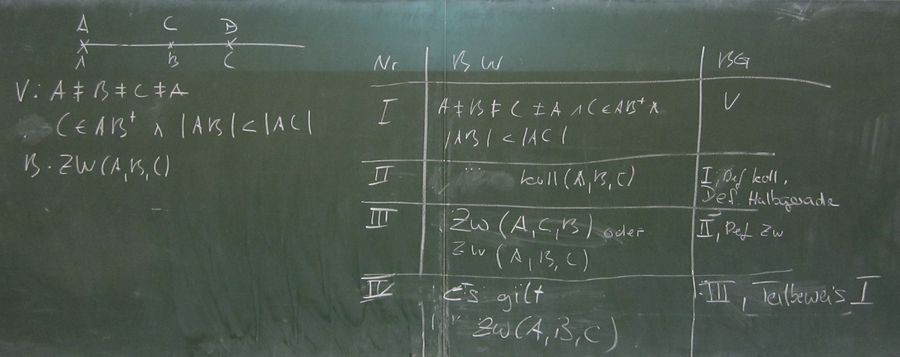
23052012 5 3 1.JPG 

Schritt III müsste eigentlich noch ergänzt werden mit der Begründung, warum nur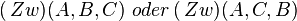 \operatorname(Zw) (A, B, C) \ oder \operatorname(Zw) (A, C, B)  

gelten kann (Definition Halbgerade; A ist Anfangspunkt).


23052012 5 3 2.JPG

--Flo60 21:33, 23. Mai 2012 (CEST)

Platz für Kommentare zu Aufgabe 5.2





Aufgabe 5.5

Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 4.3 und Zusatzaufgabe 4.4).

Ein bereitgestelltes Skript einer Übungsteilnehmerin - dankeschön

5 5 s 1.JPG

5 5 s 2.JPG

Aus der Übung

23052012 5 5.JPG


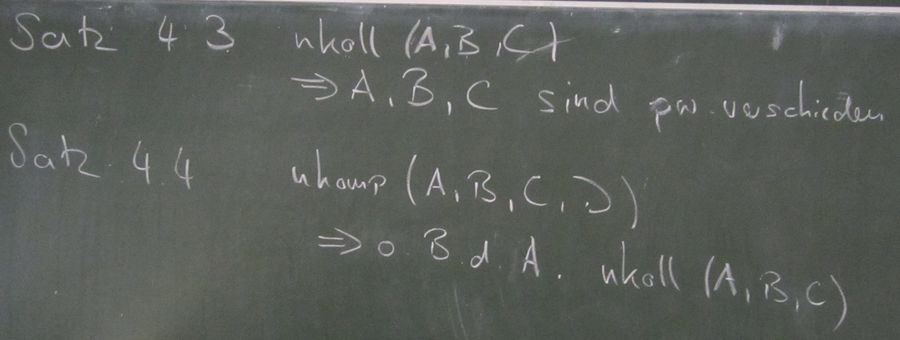
23052012 5 5 z.JPG
--Flo60 21:45, 23. Mai 2012 (CEST)

Platz für Kommentare zu Aufgabe 5.5





Zurück zur Übungsseite

Übung Aufgaben 5 S (SoSe 12)

Von „http://geometrie.zum.de/index.php?title=Lösungsideen_Übung_Heckl_23.05.2012&oldid=13817“