Übungsblatt Halbgeraden: Unterschied zwischen den Versionen
(→Lösung 2) |
(→Lösung 1) |
||
| Zeile 42: | Zeile 42: | ||
*Wir wollten <math>AB^+</math> definieren. Die Formulierung ''Es gilt <math>AB^+</math>'' hat dabei nichts verloren. | *Wir wollten <math>AB^+</math> definieren. Die Formulierung ''Es gilt <math>AB^+</math>'' hat dabei nichts verloren. | ||
*Wenn der Punkt <math>P</math> so beschaffen ist, dass der Punkt <math>B</math> zwischen <math>A</math> und <math>P</math> liegt, dann ist der Punkt <math>P</math> ein Punkt der offenen Halbgeraden <math>AB^+</math> ist zwar richtig, als Definition für <math>AB^+</math> jedoch nicht geeignet. Warum? | *Wenn der Punkt <math>P</math> so beschaffen ist, dass der Punkt <math>B</math> zwischen <math>A</math> und <math>P</math> liegt, dann ist der Punkt <math>P</math> ein Punkt der offenen Halbgeraden <math>AB^+</math> ist zwar richtig, als Definition für <math>AB^+</math> jedoch nicht geeignet. Warum? | ||
| + | |||
| + | Weil wir hier nicht das ganze der Strecke <math>AB^+</math> berücksichtigen... wir sagen hierbei nur das der punkt rechts von B liegen kann, bei der definition für AB+ gilt aber: P Element von AB oder B Element von AP--[[Benutzer:Hakunamatata|Hakunamatata]] 17:33, 19. Jul. 2012 (CEST) | ||
| + | |||
=====Lösung 2===== | =====Lösung 2===== | ||
<iframe src="http://www.ph-heidelberg.de/wp/gieding/uebungen/24_05_12/StudentSubmissions_files/Student Submissions_023.png" width="720" height="540" frameborder="2"></iframe><br /> | <iframe src="http://www.ph-heidelberg.de/wp/gieding/uebungen/24_05_12/StudentSubmissions_files/Student Submissions_023.png" width="720" height="540" frameborder="2"></iframe><br /> | ||
Aktuelle Version vom 19. Juli 2012, 16:33 Uhr
Inhaltsverzeichnis |
Das Übungsblatt im Format PDF
Die Classroompresenterfolien als PDF
Eine etwas andere Darstellung von 
Und das passende Pendant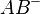 
gleich dazu
Die Videos wurden in der Tat spontan erstellt, helfen aber evtl. ein wenig fürs Verständnis. --Flo60 19:32, 10. Jun. 2011 (CEST)
Auswertung des Übungsanteils der Vorlesung vom 24. Mai 2012
Alle Folien
Die HTML-Datei mit allen Folien finden Sie hier:
http://www.ph-heidelberg.de/wp/gieding/uebungen/24_05_12/StudentSubmissions.html
Ausgewählte Kommentare
Aufgabe 1
Lösung 1
[ www.ph-heidelberg.de is not an authorized iframe site ]
perfekt --*m.g.* 07:53, 26. Mai 2012 (CEST)
Lösung 2
[ www.ph-heidelberg.de is not an authorized iframe site ]
Fehler: Von drei paarweise verschiedenen Punkten einer Geraden liegt genau einer zwischen den beiden anderen. Die zu markierenden Geradenabschnitte müssen zwangsläufig disjunkt zueinander sein. --*m.g.* 07:58, 26. Mai 2012 (CEST)
Aufgabe 2
Lösung 1
[ www.ph-heidelberg.de is not an authorized iframe site ]
perfekt --*m.g.* 08:00, 26. Mai 2012 (CEST)
Aufgabe 3
Lösung 1
[ www.ph-heidelberg.de is not an authorized iframe site ]
halb richtig:
- Strecke: Von der Idee her richtig, jedoch nicht korrekt geschrieben.
Menge aller Punkte, die zwischen
und 
liegen: Fehler beim Parsen(Syntaxfehler): \left{P|\operatorname{Zw}\left(A,P,B\right)\right}
Dazu kommt die Menge, die aus den beiden Endpunkten der Strecke besteht: Fehler beim Parsen(Syntaxfehler): \left{A,B\right}
.
Das Ganze schreibt sich zusammen wie folgt: Fehler beim Parsen(Syntaxfehler): \overline{AB}:=\left{P|\operatorname{Zw}\left(A,P,B\right)\right}\cup \left{A,B\right}
.
Das Zeichen 
steht für das logische und. Durch das logische und werden zwei Aussagen miteinander verknüpft. Eine Menge ist keine Aussage. Mengen werden vereinigt. Das entsprechende Zeichen ist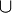 
.
Ich verstehe, wie Ihre Beschreibung der Strecke gemeint ist. Die Strecke 
ist die Menge aller Punkte, die zwischen den Punkten und liegen und dann noch der Punkt und der Punkt . Das umgangssprachliche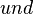 
ist so u verstehe, dass zu den Punkten, die zwischen und liegen die Endpunte der Strecke dazukommen. Dieses entspricht dem Vereinigen von Mengen und nicht der Verknüpfung zweier Aussagen durch ein logisches und.Mit den Mittel logischer Verknüpfung könnte man Strecke wie folgt ausdrücken: Fehler beim Parsen(Syntaxfehler): \overline{AB}:=\left{P| \operatorname{Zw}\left(A,P,B\right) \vee P \equiv A \vee P \equiv B \right}
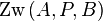ist eine Aussage: entweder liegt 
zwischen und oder nicht.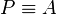 
ist ebenso entweder wahr oder falsch.
- Verlängerung von über hinaus: passt
- Alle Punkte, die mit nicht auf derselben Seite bezüglich liegen: passt
- Alle Punkte, die mit bezüglich des Punktes auf derselben Seite der Geraden liegen: Auch die Punkte der offenen Strecke liegen auf
mit auf derselben Seite von . Natürlich liegt auch der Punkt mit sich selbst bezüglich auf auf derselben Seite.
Fehler beim Parsen(Syntaxfehler): \left{P|\operatorname{Zw}\left(A,P,B\right) \vee \operatorname{Zw}\left(A,B,P\right) \vee P \equiv B \right}
Aufgabe 4
Lösung 1
[ www.ph-heidelberg.de is not an authorized iframe site ]
- Wir wollten
definieren. Die Formulierung Es gilt hat dabei nichts verloren.
- Wenn der Punkt so beschaffen ist, dass der Punkt zwischen und liegt, dann ist der Punkt ein Punkt der offenen Halbgeraden ist zwar richtig, als Definition für jedoch nicht geeignet. Warum?
Weil wir hier nicht das ganze der Strecke berücksichtigen... wir sagen hierbei nur das der punkt rechts von B liegen kann, bei der definition für AB+ gilt aber: P Element von AB oder B Element von AP--Hakunamatata 17:33, 19. Jul. 2012 (CEST)
Lösung 2
[ www.ph-heidelberg.de is not an authorized iframe site ]
Dann würde neben den Punkten der Stecke nur noch ein einziger Punkt der Geraden zur Halbgeraden gehören: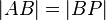 
Die Menge aller Punkte auf einer Geraden, für die nicht Zw(P,A,B) gilt, nennt man Halbgerade (AB+)--KeinKurpfälzer 21:35, 4. Jun. 2012 (CEST)
