Halbebenen und das Axiom von Pasch SS 2012: Unterschied zwischen den Versionen
Snooth (Diskussion | Beiträge) (→Definition IV.1: (offene Halbebene)) |
Snooth (Diskussion | Beiträge) (→Analogiebetrachtungen) |
||
| Zeile 38: | Zeile 38: | ||
:Es seien <math>\ g</math> eine Gerade und <math>\ T</math> ein Punkt auf ihr. Ferner sei <math>\ Q</math> ein von <math>\ T</math> verschiedener Punkt der Geraden <math>\ g</math>. Die Menge <math>\ g \setminus T</math> wird durch durch den Trenner <math>\ T</math> in genau zwei Klassen eingeteilt: | :Es seien <math>\ g</math> eine Gerade und <math>\ T</math> ein Punkt auf ihr. Ferner sei <math>\ Q</math> ein von <math>\ T</math> verschiedener Punkt der Geraden <math>\ g</math>. Die Menge <math>\ g \setminus T</math> wird durch durch den Trenner <math>\ T</math> in genau zwei Klassen eingeteilt: | ||
| − | ::# Die Menge aller Punkte von <math>\ g \setminus T</math>, die mit <math>\ Q</math> auf derselben | + | ::# Die Menge aller Punkte von <math>\ g \setminus T</math>, die mit <math>\ Q</math> auf derselben Seite bezüglich <math>T</math> liegen (<math>\ TQ^{+}</math>) . |
| − | ::# Die Menge aller Punkte von <math>\ g \setminus T</math>, die mit <math>\ Q</math> nicht auf derselben | + | ::# Die Menge aller Punkte von <math>\ g \setminus T</math>, die mit <math>\ Q</math> nicht auf derselben Seite bezüglich <math>T</math> liegen (<math>\ TQ^{-}</math>) . |
Ebenenteilung: | Ebenenteilung: | ||
:Es seien <math>\ E</math> eine Ebene und <math>\ t</math> eine Gerade, die vollständig in <math>\ E</math> liegt. Ferner sei <math>\ Q</math> ein nicht zu <math>\ t</math> gehörender Punkt der Ebene <math>\ E</math>. Die Menge <math>\ E \setminus t</math> wird durch durch den Trenner <math>\ t</math> in genau zwei Klassen eingeteilt: | :Es seien <math>\ E</math> eine Ebene und <math>\ t</math> eine Gerade, die vollständig in <math>\ E</math> liegt. Ferner sei <math>\ Q</math> ein nicht zu <math>\ t</math> gehörender Punkt der Ebene <math>\ E</math>. Die Menge <math>\ E \setminus t</math> wird durch durch den Trenner <math>\ t</math> in genau zwei Klassen eingeteilt: | ||
| − | ::# Die Menge aller Punkte von <math>\ E \setminus t</math>, die mit <math>\ Q</math> auf derselben | + | ::# Die Menge aller Punkte von <math>\ E \setminus t</math>, die mit <math>\ Q</math> auf derselben Seite bezüglich <math>t</math> liegen (<math>\ tQ^{+}</math>) . |
| − | ::# Die Menge aller Punkte von <math>\ E \setminus t</math>, die mit <math>\ Q</math> nicht auf derselben | + | ::# Die Menge aller Punkte von <math>\ E \setminus t</math>, die mit <math>\ Q</math> nicht auf derselben Seite bezüglich <math>t</math> liegen (<math>\ tQ^{-}</math>) . |
=== Definition des Begriffs der Halbebene === | === Definition des Begriffs der Halbebene === | ||
Version vom 5. Juni 2012, 22:51 Uhr
|
Halbebenen und das Axiom von PaschHalbebenenAnalogiebetrachtungen
Die folgenden Lückentexte können Sie auch als Übungsblatt im pdf-Format herunterladen: Übungsblatt Halbgeraden/-ebenen Wir konstatieren:
Geradenteilung:
Ebenenteilung:
Definition des Begriffs der HalbebeneAlles hat zwei Seiten oder grundlegende Ideen der Beschaffenheit von EbenenOffene HalbebenenDie beiden Seiten, in die die Menge der Punkte einer Ebene Obige Ausführungen können als informelle Definition des Begriffs offene Halbebene dienen. Hinsichtlich wirklicher mathematischer Exaktheit der Festlegung, was denn eine offene Halbene sein möge, bedarf es einer genauereren Erklärung, was denn darunter zu verstehen wäre, dass zwei Punkte Definition IV.1: (offene Halbebene)
--Snooth 23:33, 5. Jun. 2012 (CEST) HalbebenenVereinigt man die Menge der Punkte einer offenen Halbeben mit der Menge der Punkte der Trägergerade so erhält man eine Halbebene. Definition IV.2: (Halbebene)
Bemerkung: Für die formale Beschreibung von offenen und geschlossenen Halbebenen wird jeweils dieselbe Bezsichnung verwendet: offene Halbebene: Definition IV.3: HalbraumGegeben sei eine Ebene E und ein Raum R, der E enthält. Die Punkte des Raumes, die nicht in E liegen, bilden zwei Mengen derart, dass gilt:
Das Axiom von Pasch
Axiom III.2: Das Axiom von Pasch
Konvexe PunktmengenDefinition IV.4: (konvexe Punktmenge)
Satz IV.2
Beweis von Satz IV.2trivial (Der Leser überzeuge sich davon) Satz IV.3
Beweis von Satz IV.3Es seien zu zeigen: Der Durchschnitt der beiden Mengen
|
 eine Gerade und
eine Gerade und  ein Punkt auf ihr. Ferner sei
ein Punkt auf ihr. Ferner sei  ein von
ein von 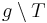 wird durch durch den Trenner
wird durch durch den Trenner 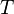 liegen (
liegen (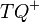 ) .
) .
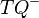 ) .
) .
 eine Ebene und
eine Ebene und 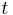 eine Gerade, die vollständig in
eine Gerade, die vollständig in 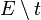 wird durch durch den Trenner
wird durch durch den Trenner  liegen (
liegen (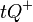 ) .
) .
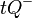 ) .
) .
 gehört u.a., dass jede Gerade
gehört u.a., dass jede Gerade  , die zu unserer jeweiligen Ebene
, die zu unserer jeweiligen Ebene 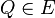 , welcher nicht zu
, welcher nicht zu 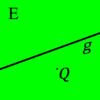
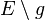 , die mit
, die mit  auf derselben Seite von
auf derselben Seite von 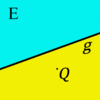
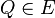 bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich
bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich  bezeichnet, die andere offene Halbebene von
bezeichnet, die andere offene Halbebene von  .
.
 und
und 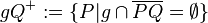
 den Trenner
den Trenner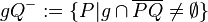
 und
und 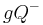 seien die beiden offenen Halbebenen von
seien die beiden offenen Halbebenen von 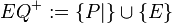
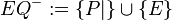
 . Ferner sei
. Ferner sei  geht. Wenn
geht. Wenn  von Punkten heißt konvex, wenn mit je zwei Punkten
von Punkten heißt konvex, wenn mit je zwei Punkten  und
und  dieser Menge die gesamte Strecke
dieser Menge die gesamte Strecke  zu
zu  und
und 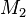 zwei konvexe Mengen.
zwei konvexe Mengen.

