Winkel SS 2012: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „=Übungsblatt= {{pdf|Uebungsblatt_01.pdf|Das Übungsblatt zur Vorlesung}} =Videos= {{#ev:youtube|z53LN9aGMOg}} {{#ev:youtube|M1pMJcQp9Is}} = Begriff des Winkels =…“) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> | ||
| + | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| + | | valign="top" | | ||
| + | |||
| + | <!--- ------------------------------------------------------------------------------------------ ---> | ||
| + | |||
=Übungsblatt= | =Übungsblatt= | ||
{{pdf|Uebungsblatt_01.pdf|Das Übungsblatt zur Vorlesung}} | {{pdf|Uebungsblatt_01.pdf|Das Übungsblatt zur Vorlesung}} | ||
| Zeile 120: | Zeile 126: | ||
::Zwei Winkel bilden ein Paar von Nebenwinkeln, wenn .... | ::Zwei Winkel bilden ein Paar von Nebenwinkeln, wenn .... | ||
| − | [[ | + | <!--- Was hier drunter steht muss stehen bleiben ---> |
| + | |} | ||
| + | </div> | ||
| + | |||
| + | [[Kategorie:Einführung_S]] | ||
Version vom 9. Juni 2012, 05:42 Uhr
|
ÜbungsblattVideosBegriff des WinkelsIdentifizieren von WinkelnRepräsentanten und GegenrepräsentantenIn welchen Fällen sind die jeweils blau gefärbten Punktmengen Modelle für Winkel?
Tabelle 1
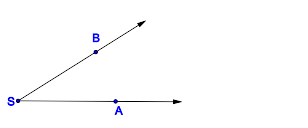
Prozess der Begriffserarbeitung als Generierung einer KlasseneinteilungIn der Didaktik bezeichnen wir die Art und Weise der Erarbeitung eines neuen Begriffs entsprechend obiger Tabelle als induktive Begriffserarbeitung: Eine gewisse Menge an Repräsentanten und Gegenrepräsentanten bezüglich des zu erarbeitenden Begriffs wird vorgegeben. Dann teilt man diese Menge in genau zwei Klassen ein. Die eine Klasse bilden alle Begriffsrepräsentanten, die andere Menge der Rest. Aufgabe: Ergänzen Sie Tabelle 1 durch weitere Repräsentanten bzw. Gegenrepräsentanten zur Erarbeitung des Winkelbegriffs. Zum besseren Verständnis: Analoge Erarbeitung des Begriffs Trapez: Realisieren von WinkelnDie Idee des konstruktiven BegriffserwerbsWährend beim induktiven Begriffserwerb das Ausgangsmaterial für den Schüler bereits vorgefertigt wurde, generiert er es sich beim konstruktiven Begriffserwerb selbst. Der gute Lehrer läßt in der Regel beide Varianten zur Anwendung kommen. Konstruktion eines WinkelsAufgabe: Zeichne einen Winkel Lösung: Definition des WinkelbegriffsDefinition V.1: (Winkel)
Arten, Winkel zu beschreiben
Die Idee des gerichteten WinkelsGerichtete Winkel werden in der Einführung in die Geometrie keine Rolle spielen. Trotzdem dürfen Sie hier ergänzen, was denn ein gerichtetet Winkel wäre.
Das Innere eines WinkelsSo ist es zu verstehen[ www.ph-heidelberg.de is not an authorized iframe site ] Definition des Inneren eines WinkelsDefinition V.2: (Inneres eines Winkels)
Satz V.1
Beweis von Satz V.1
Nullwinkel, gestreckte Winkel, überstumpfe Winkel?Bemerkung: Entsprechend Definition V.2 beinhaltet unsere Geometrie keine überstumpfen Winkel, keinen Nullwinkel und keine gestreckten Winkel. Scheitelwinkel und NebenwinkelScheitelwinkelBeispiele und GegenbeispieleSie werden den Begriff des Scheitelwinkels mit Ihren Schülern erarbeiten müssen. Entwickeln Sie ein Arbeitsblatt, das Repräsentanten und Gegenrepräsentanten bezüglich des Begriffs Scheitelwinkel enthält und binden Sie dieses in die folgende Datei ein: DefinitionDefinition V.3: (Scheitelwinkel)
NebenwinkelBeispiele und GegenbeispieleSie werden den Begriff des Nebenwinkels mit Ihren Schülern erarbeiten müssen. Entwickeln Sie ein Arbeitsblatt, das Repräsentanten und Gegenrepräsentanten bezüglich des Begriffs Scheitelwinkel enthält und binden Sie dieses in die folgende Datei ein: DefinitionDefinition V.4: (Nebenwinkel)
|
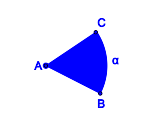
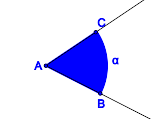
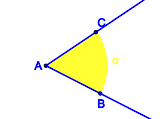
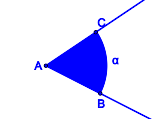
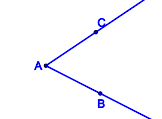
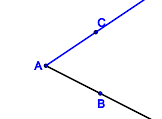
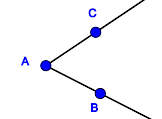
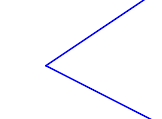
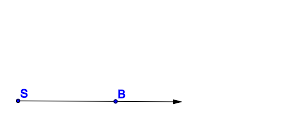
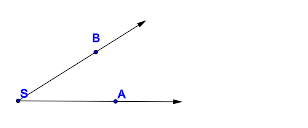
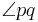 versteht man ... .
versteht man ... .
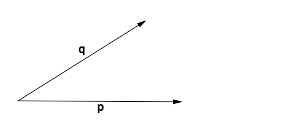
 und
und 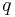 besteht.
besteht.
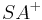 und
und 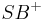 besteht.
besteht.

 ist ...
ist ...

