Lösung von Zusatzaufgabe 8.4 S: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 1: Zeile 1:
 +
==Die Aufgabe==
 
Seien <math>A, B</math> und <math>Q</math> drei paarweise verschiedene Punkte für die gelte <math>\operatorname{nkoll}(A, B, Q)</math>. Sei g eine Gerade. Beweisen Sie: <br />
 
Seien <math>A, B</math> und <math>Q</math> drei paarweise verschiedene Punkte für die gelte <math>\operatorname{nkoll}(A, B, Q)</math>. Sei g eine Gerade. Beweisen Sie: <br />
 
<math>A, B \in \ gQ^{+} \setminus g  \Rightarrow  \overline{AB}  \cap g = \emptyset</math>.<br />
 
<math>A, B \in \ gQ^{+} \setminus g  \Rightarrow  \overline{AB}  \cap g = \emptyset</math>.<br />
−
 
+
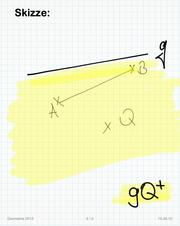
==Skizze==
−
 
+
 
[[Datei:Skizze 8.1.pdf]]<br />
 
[[Datei:Skizze 8.1.pdf]]<br />
−
Voraussetzung: <br />
+
==Voraussetzung, Behauptung==
−
(V1) <math>A\neq B\neq Q\neq A</math><br />
+
===Voraussetzung:===
−
(V2) <math>\operatorname{nkoll}(A, B, C)</math><br />
+
::(V1) <math>A\neq B\neq Q\neq A</math><br />
−
(V3) Gerade g<br />
+
::(V2) <math>\operatorname{nkoll}(A, B, C)</math><br />
−
(V4) <math>A, B \in \ gQ^{+} \setminus g</math><br />
+
::(V3) Gerade g<br />
−
Behauptung:<br />
+
::(V4) <math>A, B \in \ gQ^{+} \setminus g</math><br />
 +
===Behauptung:===
 
<math>\overline{AB}  \cap g = \emptyset</math><br />
 
<math>\overline{AB}  \cap g = \emptyset</math><br />
 
Beweis folgt..<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 19:22, 15. Jun. 2012 (CEST)
 
Beweis folgt..<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 19:22, 15. Jun. 2012 (CEST)
−
 
+
===Bemerkungen M.G.===
−
Beweis durch Widerspruch:<br />
+
Damit sind die Grundlagen für den Beweis korrekt gelegt.
 +
==Beweis durch Widerspruch==
 
Annahme: <math>\overline{AB}  \cap g \neq \emptyset</math><br />
 
Annahme: <math>\overline{AB}  \cap g \neq \emptyset</math><br />
 
Beweis:<br />
 
Beweis:<br />

Version vom 18. Juni 2012, 15:23 Uhr

Inhaltsverzeichnis

Die Aufgabe

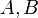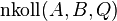Seien A, B und Q drei paarweise verschiedene Punkte für die gelte \operatorname{nkoll}(A, B, Q). Sei g eine Gerade. Beweisen Sie:
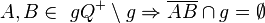A, B \in \ gQ^{+} \setminus g \Rightarrow \overline{AB} \cap g = \emptyset.

Skizze

Skizze 8.1.pdf

Voraussetzung, Behauptung

Voraussetzung:

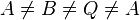
(V1) A\neq B\neq Q\neq A
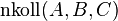
(V2) \operatorname{nkoll}(A, B, C)
(V3) Gerade g
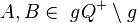
(V4) A, B \in \ gQ^{+} \setminus g

Behauptung:

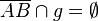
\overline{AB} \cap g = \emptyset
Beweis folgt..
--Tchu Tcha Tcha 19:22, 15. Jun. 2012 (CEST)

Bemerkungen M.G.

Damit sind die Grundlagen für den Beweis korrekt gelegt.

Beweis durch Widerspruch

Annahme: 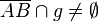\overline{AB} \cap g \neq \emptyset
Beweis:
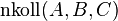1) \operatorname{nkoll}(A, B, C) (Voraussetzung)
2) Es existiert ein Dreieck 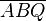\overline{ABQ} (1))
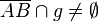3) \overline{AB} \cap g \neq \emptyset (Annahme)
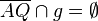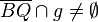4) ( \overline{AQ} \cap g = \emptyset und \overline{BQ} \cap g \neq \emptyset)

  oder

  ( \overline{BQ}  \cap g = \emptyset und \overline{AQ}  \cap g \neq \emptyset)  (3), Axiom von Pasch)

5) Widerspruch zur Voraussetzung:

   \overline{AQ}  \cap g = \emptyset und \overline{BQ}  \cap g = \emptyset  (4), Vor: A, B \in \ gQ^{+} \setminus g )


Behauptung folgt ! 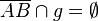\overline{AB} \cap g = \emptyset
--a.b.701 13:40, 16. Jun. 2012 (CEST)

________________________________________________________________________________________________________________________________________________________ @a.b.701: A)Muss in der Begründung in deinem Schritt 1 neben der Vor. nicht auch noch Def. I/2 stehen? B)Folgt dann im Schritt 2 logisch, dass die Punkte A,B,C ein Dreieck bilden? Oder muss man hier noch einen Zwischenschritt machen. Vielleicht über die Dreiecksungleichung als Begründung? --Luca123 18:37, 17. Jun. 2012

Ich hätte in Schritt 1 auch zusätzlich noch die Def. I/2 dazu geschrieben. Ich denke aber, dass es nicht zwingend notwendig ist, da es sich hier in diesem Fall nur aus der Voraussetzung ergibt. (?)--Sissy66 23:51, 17. Jun. 2012 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Zusatzaufgabe_8.4_S&oldid=15005“