Lösung von Aufgabe 10.4P (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie Satz IX.3: Bei einer Punktspiegelung ist der Schnittpunkt ''S'' der beiden Spiegelgeraden ''a'' und ''b'' Mittelpunkt der Strecke <math>\overline{PP'…“) |
|||
| Zeile 2: | Zeile 2: | ||
Bei einer Punktspiegelung ist der Schnittpunkt ''S'' der beiden Spiegelgeraden ''a'' und ''b'' Mittelpunkt der Strecke <math>\overline{PP''}</math>, mit <math>P''=a\circ b(P) </math>.<br /> | Bei einer Punktspiegelung ist der Schnittpunkt ''S'' der beiden Spiegelgeraden ''a'' und ''b'' Mittelpunkt der Strecke <math>\overline{PP''}</math>, mit <math>P''=a\circ b(P) </math>.<br /> | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
| + | |||
| + | |||
| + | Vor.: a verkettet b (P)=P ´´, a geschnitten b = S | ||
| + | |||
| + | Beh: S ist Mittelpunkt von PP``, also: PS=P´´S | ||
| + | |||
| + | 1. In der Vorlesung haben wir bereits bewiesen: Jeder Punkt liegt mit seinem Bildpunkt P´´= a verkettet b (P) auf einem Kreis um S. Also SP=SP´´ (Def. Mittelpunkt) | ||
| + | |||
| + | 2. P und P´´ sind e K, PSP´´ ist Durchmesser | ||
| + | |||
| + | 3. S ist Mittelpunkt von PP´´ (2.1.) q.e.d.--[[Benutzer:Geogeogeo|Geogeogeo]] 13:17, 2. Jul. 2012 (CEST) | ||
Version vom 2. Juli 2012, 12:17 Uhr
Beweisen Sie Satz IX.3:
Bei einer Punktspiegelung ist der Schnittpunkt S der beiden Spiegelgeraden a und b Mittelpunkt der Strecke 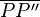 , mit
, mit 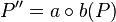 .
.
Vor.: a verkettet b (P)=P ´´, a geschnitten b = S
Beh: S ist Mittelpunkt von PP``, also: PS=P´´S
1. In der Vorlesung haben wir bereits bewiesen: Jeder Punkt liegt mit seinem Bildpunkt P´´= a verkettet b (P) auf einem Kreis um S. Also SP=SP´´ (Def. Mittelpunkt)
2. P und P´´ sind e K, PSP´´ ist Durchmesser
3. S ist Mittelpunkt von PP´´ (2.1.) q.e.d.--Geogeogeo 13:17, 2. Jul. 2012 (CEST)

