20.06.2012: Epizykloide und Asteroide: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „=Was bedeutet das?= Asteroid kommt aus dem griechischen und bedeutet: 'Sternartiger' =Konstruktion und Ideen bzgl. einer Asteroide= ==Wie sieht eine Asteroide au…“)
 
(→‎Wie konstruiere ich mir das?)
Zeile 15: Zeile 15:
 
<br /><br />
 
<br /><br />
 
Um die letzte Frage frage zu beantworten, schauen wir uns mal einen Spezialfall an:
 
Um die letzte Frage frage zu beantworten, schauen wir uns mal einen Spezialfall an:
 +
<br />
 +
Um eine bessere Verdeutlichung darstellen zu können, ist ein zusätzlicher Strahl eingezeichnet:
 +
<br />
 +
<ggb_applet width="700" height="407"  version="4.0" ggbBase64="UEsDBBQACAAIAL2e10AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAL2e10AAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7VrdbuM2Fr6ePgXhi70oxjH/Jc46UzgDDHaASVs002KxNwtZYhw2suSVZMcO+lDdV9gH2GfaQ1KyJctJnJ9pp8UGk1AiD8/h+fnOObRn/M16nqKVLkqTZ6cDcoIHSGdxnphsdjpYVpfDcPDN26/GM53P9LSI0GVezKPqdMAtpUlOB9NpHF8GKh4mAVdDDo9DxWQwFLFKmKQcX7LpAKF1ad5k+bfRXJeLKNYX8ZWeRx/zOKqc4KuqWrwZjW5ubk4aUSd5MRvNZtOTdZkMEBwzK08H9cMbYNfZdMMcOcWYjP5+/tGzH5qsrKIs1gNkVViat1+9Gt+YLMlv0I1JqitQmIV0gK60mV2BUgHnAzSyVAuwyELHlVnpEva2Xp3S1XwxcGRRZtdf+SeUbvUZoMSsTKKL0wE+YULQkBKlAoKFtDLywuisqmlJLXPUcBuvjL7xbO2TkwibqjxPp5HliH75BVFMMXptB+IHCoOUfgn7Ocz8QP3A/SA8DffbuSflnoZ7Gs4GaGVKM0316eAySkswockuC3Df9r2sNql256kndtqT16BTaW6BmGGIE29zmMf4tf2V8MvtwqirJGlJrYrlI4U2IgmT8niZ9FmaskYoV6Qvk4o79JT3CPWKH6WoaNkWRLl/7rcnkd2n5r5E//48gZL/JiqORw1WxjU8UHllaevwqfS8tIBhCgll454gAeCQAYS5QETBEFAEcEBEIC7glYRI2jFALIAFjhgKkaUjDDl0iBD+8MAxk0gAMzsbACgRAUEcCYaIAxVHACXkgAkgpQwohEACNlnxhFoWTCIu4Y2FiMMZLSYDAoQMNsI7iKeIEcTsZhIgKpG0/Ai3WJehPTqwpEhiJIllCLAGSHs4A32ImNVG1uYy2WJZdUwUz5PmscoXW18ANSSkXdrzCaqTFV+N02iqU6gUF9aTCK2i1CLCCbrMswo1TqR+blZEiysTlxe6qmBXiX6OVtHHqNLr90BdNrIdbZxn5fdFXr3L0+U8KxGK8xRvz5ynpPVMt6eGF9Za4O0F0VqQrefgoNwcVtCy1CA/L8qGPEqSD5ZilxrAkt9l6eas0NH1IjddNcYjV3TGehmnJjFR9hMEq5Vi7YJ2Ncjmq6YGiUA1J8mL5GJTQgij9T90kUOuwuQECkkoaRByRUMZDNCmXiL0hEnFAsUDJiQO4WxxZMFHiDoJBccskJxwxZnddMcarWXr1dZH0Vpv1Z8VFtq16vblQ3mWp7spZ4B30aJaFq5/gOxYWK0m2SzVLkhcvoXiHF9P8/VFna49r0+bBbxhf4DpzBkeQXKgQgBBPU796GjsybZU2NFgR4GbcDPJdp0o6ijcOPWjo4L49UerNSWNmgQ3YkzpUhoedIDjgt9W+mVmqo/NS2Xi61pT4um/Xc6nehtCXZbkhViOR3shNr7WRabTOqLBk8t8WXqAtoI90bGZw6tfqA0SWWf9CAfws4meFbo5d+o6M28ut4rbsdqbdqzeF/n8Q7b6BJHQOwC0ZwVEBxzC5n2/vNOp0WFcxoVZ2HBEU6gR13oXcYkpIygxSRt0FqDAJHYsK1NZwwF0l9VVDoHwPs0leDKBtAPTFpypnkMzhioXfy6Et544d12eNTnKpz9D5tvz1M6lsHwwFl3URuniKrKdYG2XNNroomMpx+88T/bt11gGssDCu3+htQ8cf154WAA7B7dOGgOHlGjthaJNPd76Ft+3uFZTC8FO3vaze56E8PJG6pkrW851YeKtQa6dwWDnst6/FdcxYlPw/abWue8yI24ZkRxpxJquTG0fjuYG+oohOGMegVWsU6Yl1JYKriIQ39nuKuId3ORm7Oy2to1sbUjhHi7NuhWGEFnmFnAWdWJil1oqKHvX0NyXLv9VdaZzD38zSaKz7WmPcDk+5PK2i+J8Po+yBGWu2XpnijjVg131j7ANbBQR6y5v9WXVLMSeWc2i52/AVsvb8QPweKRjH4mOp5gXiqzOVnBSKOpwKcX1lXeDG4A0M2uwztC7nNRTt6QVzuCkwqzRpKGfNFQT6EaG/onVTCe84TUR9ZM/zL8yf/7SZ3fbW5lLEz/dnwyNoGP9GvX9mjzGr0nfr89C7J/HsfhESCo+m2+/d9Wn69qk58vJ/b7slrDJQ748XMMI9V2XG7+MOiYDaG0JDQXmUgVY1WWNUZgnElbhJ6Bh8CJl7gjMTTzmyJ2Y04/BnP4/5g5jDiCHOz+kD79+aNRo7AfHM9D5Q7Q5nHYnPddH97u+AE6NX6Pf1/E7hB00l8dY3763bVFPiZ09D5j5IjWxqbaWTG0u+JBVcM/RrpXvX1+utV7YW+N32aciykr70fT+FeKuvtXdTLYW/u+/99tWCDpOsKBYhoSElNMDzSSue0mFv/7Pr0f2kwHdbyfV0e3kE/ssgp/dQj+pkS3iVta9oxCA7iTgglFFBVGKw4O4v+E95NqHa6juAfTsMTX07E9TQ0MlBROSSBZyiWVTQzmnIVZCKWhuAmU/yn7xEvpDXsGVu+cXlz8BfyiiNp32SuhfokVe/vVRhbTe8se/moC7BGTjgGEcYEoIZU1xFURgFuKAK0C34LRfa/sUtvQe4viylZhjBRWCkoAQHiga8m0plvY7MMxwwAKigkA8qxIfCqbzh4Lp/Jhg2vsA6Khg+swfA32+D3OOsOrkIatOHm/VyTOs+qJJtW3ZA5Hre5/9uP0Mhu83lrWFfHu5s3C3yTzG8p1W8wtIjZ1+s2/bzR2u+MP1m0dA68y7d2hvjw2++leJM++0f9JHdSzbTb9/59K5w3PJiIIOhFGGiaBNNgsUVoSFKmTwE9hvr36b7Laz0wNZ7uzxWe7sS8lyVRHFuhupXa8IwqgMA47DUFHM6BaGGFoFCY4KlWLEflH3Al4Ztb+fcd+R1v/h5+3/AFBLBwi9bIqifQgAAI0kAABQSwECFAAUAAgACAC9ntdA1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAL2e10C9bIqifQgAAI0kAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAFAkAAAAA" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />
 +
<br /><br />
 +
Der Drehwinkel von <math>\ MA'^{+}</math> ist so eingestellt, dass B' wieder ein Punkt des Kreises ist. Da dies viermal passiert, ist der Drehwinkel wohl insgesamt 90°.<br />
 +
Nun dreht sich der kleine Kreis genau einmal um die eigene Achse.<br />
 +
==Welchen Radius muss der kleine Kreis haben?==
 +
Dazu nutzen wir die Berechnung am Einheitskreis. Wenn der kleine Kreis einen Umfang besitzt, der genau so groß ist, wie 1/4 Kreisbogen des großen Kreises gilt folgendes: <math>2r_k* \pi = \frac{1}{4} 2r_g* \pi  <br />
 +
2r_k* \pi = \frac{1}{4} 2*(1)* \pi <br />
 +
r_k = \frac{1}{4}*(1)</math><br /><br />
 +
Natürlich ginge das auch ohne Einheitskreis, aber in der Vorstellung wird es wohl einfacher vorstellbar sein.<br /><br /> Weiteres folgt! --[[Benutzer:HecklF|Flo60]] 20:05, 23. Jun. 2012 (CEST)

Version vom 23. Juni 2012, 19:05 Uhr

Inhaltsverzeichnis

Was bedeutet das?

Asteroid kommt aus dem griechischen und bedeutet: 'Sternartiger'

Konstruktion und Ideen bzgl. einer Asteroide

Wie sieht eine Asteroide aus?

So:

Wie konstruiere ich mir das?

Zunächst ist es sinnvoll zu betrachten, was hier überhaupt los ist:

  • Wir haben einen kleinen Kreis, der innerhalb eines größeren Kreises abrollt. Ein fixer Punkt auf dem Kreis (B') hinterlässt seine Spuren!
  • Der kleine Kreis dreht sich ganz offensichtlich viermal im Laufe der Zeit, in der der kleine Kreis das innere des großen Kreise umlaufen hat (das kann man sich bildhaft darstellen: Im Laufe der Zeit, die die Erde braucht um einemal um die Sonne zu tigern (also in der Regel schafft sie es innerhalb eines Jahres) (vgl. kleiner Kreis im großen Kreis) dreht sie sich 365 mal um sich selbst (kleiner Kreis dreht sich um sich selbst)
  • Wie hängen nun einzelne Drehwinkel zusammen?



Um die letzte Frage frage zu beantworten, schauen wir uns mal einen Spezialfall an:
Um eine bessere Verdeutlichung darstellen zu können, ist ein zusätzlicher Strahl eingezeichnet:



Der Drehwinkel von 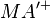\ MA'^{+} ist so eingestellt, dass B' wieder ein Punkt des Kreises ist. Da dies viermal passiert, ist der Drehwinkel wohl insgesamt 90°.
Nun dreht sich der kleine Kreis genau einmal um die eigene Achse.

Welchen Radius muss der kleine Kreis haben?

Dazu nutzen wir die Berechnung am Einheitskreis. Wenn der kleine Kreis einen Umfang besitzt, der genau so groß ist, wie 1/4 Kreisbogen des großen Kreises gilt folgendes: 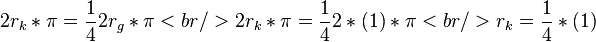2r_k* \pi = \frac{1}{4} 2r_g* \pi <br /> 2r_k* \pi = \frac{1}{4} 2*(1)* \pi <br /> r_k = \frac{1}{4}*(1)

Natürlich ginge das auch ohne Einheitskreis, aber in der Vorstellung wird es wohl einfacher vorstellbar sein.

Weiteres folgt! --Flo60 20:05, 23. Jun. 2012 (CEST)

Von „http://geometrie.zum.de/index.php?title=20.06.2012:_Epizykloide_und_Asteroide&oldid=15309“