Lösung von Zusatzaufgabe 10.1 S: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 3: | Zeile 3: | ||
Wenn in einem Dreieck zwei Innenwinkel kongruent sind, dann sind zwei Seiten kongruent.<br /> | Wenn in einem Dreieck zwei Innenwinkel kongruent sind, dann sind zwei Seiten kongruent.<br /> | ||
| − | b) Vor. <math>a \tilde {=} b</math> <br /> | + | b) Skizze folgt..<br /> |
| − | Beh.: <math>\alpha \tilde {=} \beta</math> | + | |
| + | Vor. <math>a \tilde {=} b</math> <br /> | ||
| + | Beh.: <math>\alpha \tilde {=} \beta</math> <br /> | ||
(1) <math>a \tilde {=} c</math> // Vor. <br /> | (1) <math>a \tilde {=} c</math> // Vor. <br /> | ||
Version vom 30. Juni 2012, 12:25 Uhr
Versuch Lerngruppe Nummero6/Tchu Tcha Tcha:
a) Wenn in einem Dreieck zwei Seiten kongruent sind, dann sind die Basiswinkel kongruent.
Wenn in einem Dreieck zwei Innenwinkel kongruent sind, dann sind zwei Seiten kongruent.
b) Skizze folgt..
Vor.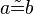 
Beh.: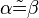 
(1) 
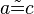// Vor.
(2) es existiert w (die WH von 
) // Ex. & Eind. der WH
(3) Fehler beim Parsen(Syntaxfehler): \ w \cap \overline{AB} = \{S}
// Vor., (1), Lemma 1
(4) Fehler beim Parsen(Syntaxfehler): \left| \angle ACS \right| \tilde {=} \left| \angle DCS \right| \tilde
// (2),(3)
(5) 
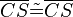// trivial, Vor., (3)
(6) 
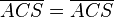// (1),(4),(5), SWS
(7) 
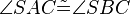// (6), Dreieckskongruenz
(8) Beh. stimmt // (7)
qed
--Tchu Tcha Tcha 12:55, 30. Jun. 2012 (CEST)
