Lösung von Aufg. 11.4 S: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „== Aufgabe 11.4 == Beweisen Sie: Sei <math>\overline{ABC} </math> ein Dreieck mit schulüblichen Bezeichnungen. Es gilt:<br /> <math>\left| \alpha \right| > \left…“) |
(→Aufgabe 11.4) |
||
| Zeile 4: | Zeile 4: | ||
<br /><br /> | <br /><br /> | ||
Hinweis: Indirekt (durch Widerspruchsbeweis) in wenigen Schritten machbar!<br /> | Hinweis: Indirekt (durch Widerspruchsbeweis) in wenigen Schritten machbar!<br /> | ||
| + | <br /> | ||
| + | Lösungsversuch Nummero6/Tchu Tcha Tcha:<br /> | ||
| + | Vor.: <math>\left| \alpha \right| > \left| \beta \right| </math><br /> | ||
| + | Beh.: <math>\left| a \right| > \left| b \right|</math><br /> | ||
| + | Annahme 1: <math>\left| a \right|</math> = <math> \left| b \right|</math><br /> | ||
| + | Annahme 2: <math>\left| a \right| < \left| b \right|</math><br /> | ||
| + | |||
| + | (1) Wenn <math>\left| a \right| = \left| b \right|</math> (Ann.1), dann gilt nach dem BWS: <math>\left| \alpha \right| = \left| \beta \right| </math><br /> | ||
| + | (2) Widerspruch zur Voraussetzung, Annahme 1 ist zu verwerfen // (1), Vor.<br /> | ||
| + | Hat jemand eine Idee, wie ich Annahme 2 begründen kann?!? | ||
| + | --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 17:30, 6. Jul. 2012 (CEST) | ||
[[Kategorie:Einführung_S]] | [[Kategorie:Einführung_S]] | ||
Version vom 6. Juli 2012, 16:30 Uhr
Aufgabe 11.4
Beweisen Sie: Sei 
ein Dreieck mit schulüblichen Bezeichnungen. Es gilt:
Hinweis: Indirekt (durch Widerspruchsbeweis) in wenigen Schritten machbar!
Lösungsversuch Nummero6/Tchu Tcha Tcha:
Vor.: 
Beh.: 
Annahme 1: 
= 
Annahme 2: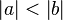 
(1) Wenn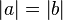 
(Ann.1), dann gilt nach dem BWS: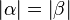 
(2) Widerspruch zur Voraussetzung, Annahme 1 ist zu verwerfen // (1), Vor.
Hat jemand eine Idee, wie ich Annahme 2 begründen kann?!?
--Tchu Tcha Tcha 17:30, 6. Jul. 2012 (CEST)
