Lösung von Testaufgabe 01: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 3: | Zeile 3: | ||
Es sei <math> \overline{LMNO} </math> ein Viereck. Wenn in diesem Viereck die Diagonalen orthogonal zueinander sind, dann ist dieses Viereck ein gemeines Scherenwagenheberviereck.--[[Benutzer:LuLu7410|LuLu7410]] 21:12, 8. Jul. 2012 (CEST)<br /> | Es sei <math> \overline{LMNO} </math> ein Viereck. Wenn in diesem Viereck die Diagonalen orthogonal zueinander sind, dann ist dieses Viereck ein gemeines Scherenwagenheberviereck.--[[Benutzer:LuLu7410|LuLu7410]] 21:12, 8. Jul. 2012 (CEST)<br /> | ||
| − | Ein konvexes Viereck, dessen Diagonalen senkrecht aufeinander stehen, nennt man gemeines Scherenwagenheberviereck.--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 21:28, 8. Jul. 2012 (CEST) | + | Ein konvexes Viereck, dessen Diagonalen senkrecht aufeinander stehen, nennt man gemeines Scherenwagenheberviereck.--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 21:28, 8. Jul. 2012 (CEST)<br/> |
| + | <br/> | ||
| + | @Tchu Tcha Tcha: Hätte ich jetzt auch so gesagt.--[[Benutzer:RitterSport|RitterSport]] 10:51, 10. Jul. 2012 (CEST) | ||
Version vom 10. Juli 2012, 09:51 Uhr
Definitionsversuch gemeines Scherenwagenheberviereck:
Es sei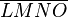 
ein Viereck. Wenn in diesem Viereck die Diagonalen orthogonal zueinander sind, dann ist dieses Viereck ein gemeines Scherenwagenheberviereck.--LuLu7410 21:12, 8. Jul. 2012 (CEST)
Ein konvexes Viereck, dessen Diagonalen senkrecht aufeinander stehen, nennt man gemeines Scherenwagenheberviereck.--Tchu Tcha Tcha 21:28, 8. Jul. 2012 (CEST)
@Tchu Tcha Tcha: Hätte ich jetzt auch so gesagt.--RitterSport 10:51, 10. Jul. 2012 (CEST)
